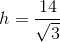How to find the length of the diagonal of a hexagon
Help Questions
ACT Math › How to find the length of the diagonal of a hexagon
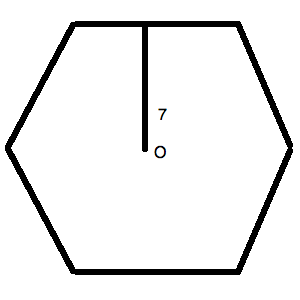
The figure above is a regular hexagon. O is the center of the figure. The line segment makes a perpendicular angle with the external side.
What is the length of the diagonal of the regular hexagon pictured above?
Explanation
You could redraw your figure as follows. Notice that this kind of figure makes an equilateral triangle within the hexagon. This allows you to create a useful 

The 
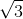


Therefore, we can say:
Solve for 
Rationalize the denominator:
Now, the diagonal of a regular hexagon is actually just double the length of this hypotenuse. (You could draw another equilateral triangle on the bottom and duplicate this same calculation set—if you wanted to spend extra time without need!) Thus, the length of the diagonal is:
The perimeter of a regular hexagon is 
Explanation
To begin, calculate the side length of the hexagon. Since it is regular, its sides are of equal length. This means that a given side is 

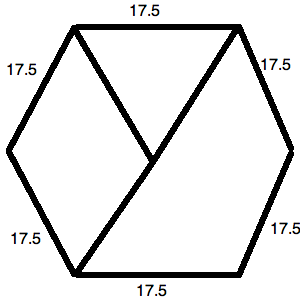
The little triangle at the top forms an equilateral triangle. This means that all of its sides are