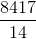All ACT Math Resources
Example Questions
Example Question #14 : How To Evaluate A Fraction
Simplify:
Begin by simplifying the numerator.


Now, in our original problem this is really is:
When you divide by a fraction, you really multiply by the reciprocal:
Example Question #15 : How To Evaluate A Fraction
Simplify:
Begin by simplifying the numerator and the denominator.
Numerator


Denominator


Now, reconstructing our fraction, we have:
To make this division work, you multiply the numerator by the reciprocal of the denominator:
Example Question #31 : Algebraic Fractions
Simplify:
None of the other answer choices are correct.
Recall that dividing is equivalent multiplying by the reciprocal. Therefore, ((x - 4) / (1 / 2)) / (1 / (x + 4)) = ((x - 4) * 2) * (x + 4) / 1.
Let's simplify this further:
(2x – 8) * (x + 4) = 2x2 – 8x + 8x – 32 = 2x2 – 32
Example Question #16 : How To Evaluate A Fraction
Solve for 
Begin by isolating the variables:
Now, the common denominator of the variable terms is 

Simplify:
Cross-multiply:
Simplify:
Finally, solve for 
Example Question #2 : How To Evaluate A Fraction
Evaluate ![]() when x=11. Round to the nearest tenth.
when x=11. Round to the nearest tenth.
1.9
0.3
1.8
0.2
1.8
Wherever there is an x, plug in 11 and perform the given operations. The numerator will be equal to 83 and the denominator will be equal to 46. 83 divided by 46 is equal to 1.804… and since the second decimal place is not greater than or equal to 5, the first decimal place stays the same when rounding so the final answer is 1.8.
Example Question #3 : Algebraic Fractions
Find the inverse equation of:
To solve for an inverse, we switch x and y and solve for y. Doing so yields:
Example Question #4 : Algebraic Fractions
Find the inverse equation of 
1. Switch the 

2. Solve for 
Example Question #5 : Algebraic Fractions



When 

If 



If 


1. Using any of the two 

Using 
2. Use your new equation 

Example Question #6 : Algebraic Fractions
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
If 


An inverse variation is a function in the form: 


Substitute each 

Therefore, the constant of variation, 




Example Question #1 : How To Find Inverse Variation
Two numbers 





If 




All ACT Math Resources