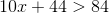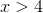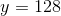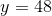All TACHS Math Resources
Example Questions
Example Question #1 : Algebra
Solve the following inequality:
In algebra an inequality is a relationship that holds through different values of a variable. An inequality is considered to be solved when the variable is isolated to one side of the inequality. We will do this by performing the reverse of the operations that were done to the variable. It is important to note that what is done to one side of the inequality needs to be done on the other.
Let's start by writing the inequality.

Subtract 
Divide each side of the inequality by 
Solve.
The variable is greater than four.
Example Question #2 : Algebra
Solve for 
In order to solve this problem we need isolate the variable on the left side o the equation. We will do this by performing the reverse of the operations that were done to the variable. It is important to note that what is done to one side of the equation needs to be done on the other.
Let's start by writing the equation.
Subtract 
Multiply both sides of the equation by 
Solve.
Example Question #1 : One Variable Equations
Solve for 
Start by subtracting 
Next, add 
Finally, divide both sides by 
Example Question #2 : One Variable Equations
Solve for 
Start by subtracting both sides by 
Next, subtract both sides by 
Finally, divide both sides by 
Example Question #2 : Algebra
What value of 
Isolate the 

Multiplication precedes addition in the order of operations, so reverse the addition of 16 by subtracting 16 from both sides:
Now reverse multiplication by 2 by dividing by 2:
All TACHS Math Resources