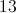Cubes
Help Questions
SAT Math › Cubes
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
100
200
500
750
1000
Explanation
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
Find the surface area of a cube given side length of 3.
Explanation
To find the surface area of a cube means to find the area around the entire object. In the case of a cube, we will need to find that area of all the sides and the top and bottom. Since a cube has equal side lengths, the area of each side and the area of the top and bottom will all be the same.
Recall that the area for a side of a cube is:
From here there are two approaches one can take.
Approach one:
Add all the areas together.
Approach two:
Use the formula for the surface area of a cube,
In this particular case we are given the side length is 3.
Thus we can find the surface area to be,
by approach one,
and by appraoch two,

A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
Explanation
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
A certain cube has a side length of 25 m. How many square tiles, each with an area of 5 m2, are needed to fully cover the surface of the cube?
100
200
500
750
1000
Explanation
A cube with a side length of 25m has a surface area of:
25m * 25m * 6 = 3,750 m2
(The surface area of a cube is equal to the area of one face of the cube multiplied by 6 sides. In other words, if the side of a cube is s, then the surface area of the cube is 6_s_2.)
Each square tile has an area of 5 m2.
Therefore, the total number of square tiles needed to fully cover the surface of the cube is:
3,750m2/5m2 = 750
Note: the volume of a cube with side length s is equal to _s_3. Therefore, if asked how many mini-cubes with side length n are needed to fill the original cube, the answer would be:
s3/n3
A rectangular prism has a volume of 144 and a surface area of 192. If the shortest edge is 3, what is the length of the longest diagonal through the prism?
Explanation
The volume of a rectangular prism is 
We are told that the shortest edge is 3. Let us call this the height.
We now have 

Now we replace variables by known values:
Now we have:
We have thus determined that the other two edges of the rectangular prism will be 4 and 12. We now need to find the longest diagonal. This is equal to:
If you do not remember how to find this directly, you can also do it in steps. You first find the diagonal across one of the sides (in the plane), by using the Pythagorean Theorem. For example, we choose the side with edges 3 and 4. This diagonal will be:
We then use a plane with one side given by the diagonal we just found (length 5) and the other given by the distance of the 3rd edge (length 12).
This diagonal is then 
Find the surface area of a cube given side length of 3.
Explanation
To find the surface area of a cube means to find the area around the entire object. In the case of a cube, we will need to find that area of all the sides and the top and bottom. Since a cube has equal side lengths, the area of each side and the area of the top and bottom will all be the same.
Recall that the area for a side of a cube is:
From here there are two approaches one can take.
Approach one:
Add all the areas together.
Approach two:
Use the formula for the surface area of a cube,
In this particular case we are given the side length is 3.
Thus we can find the surface area to be,
by approach one,
and by appraoch two,

Find the surface area of a cube with side length 2.
Explanation
To solve, simply use the formula for the surface area of a cube. Thus,
Find the surface area of a cube with side length 2.
Explanation
To solve, simply use the formula for the surface area of a cube. Thus,
Find the volume of a cube given side length is 1.
Explanation
To solve, simply use the formula for the volume of a cube. Thus,
What is the volume of a cube with a side length of 7.5 cm?
(Round two the nearest two places)
Explanation
The formula for volume of a cube is,
where

The side length of the cube is given as 7.5cm.
Substituting this into the formula for a cube's volume is as follows.