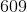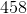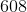All SAT Math Resources
Example Questions
Example Question #1 : Other Arithmetic Sequences
The first, third, fifth and seventh terms of an arithmetic sequence are 




The first important thing to note is that the way these answer choices are set up, any answer that does not have a 


Example Question #8 : Other Arithmetic Sequences
Find the unknown term in the sequence:
The pattern in this sequence is 



Then, our third term must be:

Example Question #9 : Other Arithmetic Sequences
An arithmetic sequence begins as follows:
Give the first integer in the sequence.
The sequence has no integers.
The sequence has no integers.
Rewrite all three fractions in terms of their least common denominator, which is 


The sequence begins
Subtract the first term 


Setting 

If this common difference is added a few more times, a pattern emerges:

All of the denominators end in 4 or 9, so none of them can be divisible by 20. Therefore, none of the terms will be integers.
Example Question #21 : Sequences
An arithmetic sequence begins as follows:
What is the first positive number in the sequence?
The twenty-third term
The twentieth term
The nineteenth term
The twenty-second term
The twenty-first term
The twentieth term
Given the first two terms 


Setting 

The 
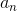
Since we are looking for the first positive number - equivalently, the first number greater than 0:


Setting 


Since 



Example Question #11 : Other Arithmetic Sequences
An arithmetic sequence begins as follows:
Give the thirteenth term of the sequence as a fraction in lowest terms.
Subtract the first term 


Setting 

The 
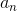
Setting 


As a fraction, this is
Example Question #11 : Arithmetic Sequences
2, 8, 14, 20
The first term in the sequence is 2, and each following term is determined by adding 6. What is the value of the 50th term?
300
296
320
302
296
We start by multiplying 6 times 46, since the first 4 terms are already listed. We then add the product, 276, to the last listed term, 20. This gives us our answer of 296.
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
Which of the following could not be a term in the sequence 5, 10, 15, 20...?
35
3751
2500
10005
3751
All answers in the sequence must end in a 5 or a 0.
Example Question #1 : Nth Term Of An Arithmetic Sequence
In an arithmetic sequence, each term is two greater than the one that precedes it. If the sum of the first five terms of the sequence is equal to the difference between the first and fifth terms, what is the tenth term of the sequence?
–0.6
0.6
2.4
15.6
10
15.6
Let a1 represent the first term of the sequence and an represent the nth term.
We are told that each term is two greater than the term that precedes it. Thus, we can say that:
a2 = a1 + 2
a3 = a1 + 2 + 2 = a1 + 2(2)
a4 = a1 + 3(2)
a5 = a1 + 4(2)
an = a1 + (n-1)(2)
The problem tells us that the sum of the first five terms is equal to the difference between the fifth and first terms. Let's write an expression for the sum of the first five terms.
sum = a1 + (a1 + 2) + (a1 + 2(2)) + (a1 + 3(2)) + (a1 + 4(2))
= 5a1 + 2 + 4 + 6 + 8
= 5a1 + 20
Next, we want to write an expression for the difference between the fifth and first terms.
a5 - a1 = a1 + 4(2) – a1 = 8
Now, we set the two expressions equal and solve for a1.
5a1 + 20 = 8
Subtract 20 from both sides.
5a1 = –12
a1 = –2.4.
The question ultimately asks us for the tenth term of the sequence. Now, that we have the first term, we can find the tenth term.
a10 = a1 + (10 – 1)(2)
a10 = –2.4 + 9(2)
= 15.6
The answer is 15.6 .
Example Question #1 : Nth Term Of An Arithmetic Sequence
In a certain sequence, an+1 = (an)2 – 1, where an represents the nth term in the sequence. If the third term is equal to the square of the first term, and all of the terms are positive, then what is the value of (a2)(a3)(a4)?
72
24
6
63
48
48
Let a1 be the first term in the sequence. We can use the fact that an+1 = (an)2 – 1 in order to find expressions for the second and third terms of the sequence in terms of a1.
a2 = (a1)2 – 1
a3 = (a2)2 – 1 = ((a1)2 – 1)2 – 1
We can use the fact that, in general, (a – b)2 = a2 – 2ab + b2 in order to simplify the expression for a3.
a3 = ((a1)2 – 1)2 – 1
= (a1)4 – 2(a1)2 + 1 – 1 = (a1)4 – 2(a1)2
We are told that the third term is equal to the square of the first term.
a3 = (a1)2
We can substitute (a1)4 – 2(a1)2 for a3.
(a1)4 – 2(a1)2 = (a1)2
Subtract (a1)2 from both sides.
(a1)4 – 3(a1)2 = 0
Factor out (a1)2 from both terms.
(a1)2 ((a1)2 – 3) = 0
This means that either (a1)2 = 0, or (a1)2 – 3 = 0.
If (a1)2 = 0, then a1 must be 0. However, we are told that all the terms of the sequence are positive. Therefore, the first term can't be 0.
Next, let's solve (a1)2 – 3 = 0.
Add 3 to both sides.
(a1)2 = 3
Take the square root of both sides.
a1 = ±√3
However, since all the terms are positive, the only possible value for a1 is √3.
Now, that we know that a1 = √3, we can find a2, a3, and a4.
a2 = (a1)2 – 1 = (√3)2 – 1 = 3 – 1 = 2
a3 = (a2)2 – 1 = 22 – 1 = 4 – 1 = 3
a4 = (a3)2 – 1 = 32 – 1 = 9 – 1 = 8
The question ultimately asks for the product of the a2, a3, and a4, which would be equal to 2(3)(8), or 48.
The answer is 48.
Example Question #21 : Sequences
In the given sequence, the first term is 3 and each term after is one less than three times the previous term.
What is the sixth term in the sequence?
The fourth term is: 3(23) – 1 = 69 – 1 = 68.
The fifth term is: 3(68) – 1 = 204 – 1 = 203.
The sixth term is: 3(203) – 1 = 609 – 1 = 608.
Certified Tutor
Certified Tutor
All SAT Math Resources