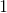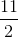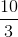All SAT Math Resources
Example Questions
Example Question #1 : How To Find The Slope Of Parallel Lines
Consider line c to be y= -4x - 7. Which is the reflection of line c across the x-axis?
y = 4x + 7
y = –4x + 7
y = (1/4)x + 7
y = 4x – 7
y = 4x + 7
A line reflected across the x-axis will have the negative value of the slope and intercept. This leaves y= 4x + 7.
Example Question #1 : How To Find The Slope Of Parallel Lines
If line J passes through the points (1, 3) and (2, 4) and line K passes through (0, x) and (10, 3), what would be the value of x in order for lines J and K to be parallel?
7
–13
13
–7
1
–7
Find the slope of line J, (4 – 3)/(2 – 1) = 1
Now use this slope in for the equation of line K of the form y = mx + b for the other point (10, 3)
3 = 10 + b → b = –7
So for the point (0, X) → X = 0 – 7,
so x = –7 when these two lines are parallel.
Example Question #2 : How To Find The Slope Of Parallel Lines
Line 

If line 





We are told that lines l and m are parallel. This means that the slope of line m must be the same as the slope of l. Line l is written in the standard form of Ax + By = C, so its slope is equal to –A/B, or –2/–3, which equals 2/3. Therefore, the slope of line m must also be 2/3.
We are told that line m passes through the points (1, 4) and (2, a). The slope between these two points must equal 2/3. We can use the formula for the slope between two points and then set this equal to 2/3.
![]()
slope = (a – 4)/(2 – 1) = a – 4 = 2/3
a – 4 = 2/3
Multiply both sides by 3:
3(a – 4) = 2
3a – 12 = 2
Add 12 to both sides:
3a = 14
a = 14/3
Example Question #32 : Coordinate Plane
What is the slope of a line parallel to the line: -15x + 5y = 30 ?
1/3
30
3
-15
3
First, put the equation in slope-intercept form: y = 3x + 6. From there we can see the slope of this line is 3 and since the slope of any line parallel to another line is the same, the slope will also be 3.
Example Question #3 : How To Find The Slope Of Parallel Lines
What is the slope of any line parallel to –6x + 5y = 12?
12
12/5
6/5
5/6
6
6/5
This problem requires an understanding of the makeup of an equation of a line. This problem gives an equation of a line in y = mx + b form, but we will need to algebraically manipulate the equation to determine its slope. Once we have determined the slope of the line given we can determine the slope of any line parallel to it, becasue parallel lines have identical slopes. By dividing both sides of the equation by 5, we are able to obtain an equation for this line that is in a more recognizable y = mx + b form. The equation of the line then becomes y = 6/5x + 12/5, we can see that the slope of this line is 6/5.
Example Question #4 : How To Find The Slope Of Parallel Lines
What is the slope of a line that is parallel to the line 11x + 4y - 2 = 9 – 4x ?
We rearrange the line to express it in slope intercept form.
Any line parallel to this original line will have the same slope.
Example Question #5 : How To Find The Slope Of Parallel Lines
In the standard (x, y) coordinate plane, what is the slope of a line parallel to the line with equation 
Parallel lines will have equal slopes. To solve, we simply need to rearrange the given equation into slope-intercept form to find its slope.
The slope of the given line is 

Example Question #6 : How To Find The Slope Of Parallel Lines
What is the slope of a line that is parallel to the line 
Parallel lines have the same slope. The question requires you to find the slope of the given function. The best way to do this is to put the equation in slope-intercept form (y = mx + b) by solving for y.
First subtract 6x on both sides to get 3y = –6x + 12.
Then divide each term by 3 to get y = –2x + 4.
In the form y = mx + b, m represents the slope. So the coefficient of the x term is the slope, and –2 is the correct answer.
Example Question #2 : How To Find The Slope Of Parallel Lines
Solve each problem and decide which is the best of the choices given.
What is the slope of a line parallel to the following equation of a line?
Parallel lines have the same slope. So to find the slope of the given equation by getting the equation in slope-intercept form 

First, subtract both sides by 

A parallel line would have a slope of 
Example Question #3 : How To Find The Slope Of Parallel Lines
Which of the following lines is parallel to 
None of the given answers
Remember that in order for two lines to be parallel, their slopes must be the same.
In slope-intercept form, a line's slope 

For our given line, the slope, therefore, is 


Therefore, 
All SAT Math Resources