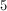All SAT Math Resources
Example Questions
Example Question #3032 : Sat Mathematics
If x > 0, what is the median of the set of numbers?
{x + 2, x – 4, x + 6, x – 8}
x + 2
x – 1
x + 6
x + 1
x – 4
x – 1
To find the median, you need to find the middle number of the ordered list. Since there are four numbers in the list, you need to average the two middle numbers.
Ordered list = {x – 8, x – 4, x + 2, x + 6}
((x – 4) + (x + 2))/2 = (2x – 2)/2 = x – 1
Example Question #11 : Median
A car travels at 60 miles per hour for 3 hours, 55 miles per hour for 2 hours, and 40 miles per hour for 3 hours. What (to the closest hundreth) is its average speed over the whole course of this trip?
51.67 miles per hour
55 miles per hour
58.13 miles per hour
51.25 miles per hour
19.38 miles per hour
51.25 miles per hour
The easiest way to solve this is to find the total number of miles traveled by the car and divide that by the total time travelled.
Recall that D = rt; therefore, for each of these three periods, we can calculate the distance and sum those products:
Dtotal = 60 * 3 + 55 * 2 + 40 * 3 = 180 + 110 + 120 = 410
The total amount of time travelled is: 3 + 2 + 3 = 8
Therefore, the average rate is 410 / 8 = 51.25 miles per hour.
Example Question #3031 : Sat Mathematics
Set S consists of a set of six positive consecutive odd integers. Set T consists of the squares of each of the six elements in S. If the range of T is 560, then what is the median of T?
785
788
784
729
841
785
Let's let a and b stand for the smallest and largest values in S, respectively. Because T is equal to the square of the elements in S, then the smallest and largest values in T will be equal to a2 and b2 , respectively.
We are told that the range of T is equal to 560. The range of a set of numbers is the difference between the largest and smallest, which in this case we can represent as b2 – a2. We can now write the following equation:
b2 – a2 = 560
Noice that b2 – a2 can be factored as (b – a)(b + a), which is the formula for the difference of squares.
(b – a)(b + a) = 560
Notice that the value b – a represents the range of S, because it is the difference between the largest and smallest values of S.
We are told that S consists of six consecutive odd integers. We can use this information to find the range of S. Because they are consecutive odd integers, each member in S will be two larger than the one before it. Thus, we could represent S as follows:
a, a + 2, a + 4, a + 6, a + 8, a + 10
The range of S is equal (a + 10) – a = 10. Thus, b – a must equal 10.
Let's go back to the equation (b – a)(b + a) = 560. We can replace b – a with 10 and solve for b + a.
(10)(b + a) = 560
Divide both sides by 10.
b + a = 56
So, we know that b – a = 10, and b + a = 56. We can solve this system of equations to find the values of a and b, which will give us the smallest and largest values in S.
Let's solve the first equation in terms of b.
b – a = 10
Add a to both sides.
b = 10 + a
Now we can substitute 10 + a in for b in the second equation.
(10 + a) + a = 56
10 + 2a = 56
Subtract 10 from both sides.
2a = 46
Divide both sides by 2.
a = 23
b = 10 + a = 10 + 23 = 33
The smallest value of S is 23, and the largest value is 33. Thus, S consists of the following set:
23, 25, 27, 29, 31, 33
We are told that T is equal to the squares of the elements of S. Thus, T consists of the following numbers:
529, 625, 729, 841, 961, 1089
We are asked ultimately to find the median of T. The median of any set is the middle number. In this case, T has six elements, so there are actually two numbers in the middle: 729 and 841. To find the median, we will take the average of the two middle numbers. The average of two numbers is equal to their sum divided by two.
median of T = (729 + 841)/2 = 1570/2 = 785.
The answer is 785.
Example Question #3031 : Sat Mathematics
The median of a set of eight consecutive odd integers is 22. What is the largest integer in the set?
31
33
25
29
27
29
The set consists of eight consecutive odd integers. Let's call the integers, in order from least to greatest, A, B, C, D, E, F, G, and H. We are told that the median of the set is 22. The median in a set of numbers is the number in the middle. In the set of A, B, C, D, E, F, G, and H, the numbers represented by D and E would be in the middle. When we have two members in the middle, the median is equal to their average. Thus, 22 is equal to the average of D and E. In other words, 22 is the average of the 4th and 5th numbers in the set. Since 22 is halfway between 21 and 23, it makes sense that the 4th and 5th numbers would have to be 21 and 23, respectively. Thus, our set looks like this:
A, B, C, 21, 23, F, G, H
Beacuse the set consists of consecutive odd integers, each integer is two larger than the one before it. Therefore, this is the set of integers:
15, 17, 19, 21, 23, 25, 27, 29
The problem asks us to find the largest integer in the set, which is 29.
The answer is 29.
Example Question #71 : Statistics
Find the median
To find the median, arrange the numbers from lowest to highest then find the middle number.
There are two numbers in the middle in this set (

In this case, the median is 6 but you would typically find the average of the two numbers in the middle.
Example Question #12 : How To Find Median
x is the median of this set of numbers: x, 7, 12, 15, 19, 20, 8. What is one possible value of x?
16
18
11
17
14
14
The median is the "middle number" in a sorted list of number; therefore, reorder the numbers in numerical order: 7, 8, 12, 15, 19, 20. Since x is the middle number, it must come between 12 and 15, leaving 14 as the only viable choice.
Example Question #11 : How To Find Median
Craig has a jar full of loose change. He has 20 quarters, 15 dimes, 35 nickels and 55 pennies. If he orders them all from least to most valuable, what is the value of the median coin?
The median is the coin which has an equal number of coins of lesser or equal value and greater or equal value on either side of it. The median therefore falls to one of the nickels (62 quarters, dimes and nickels above it and 62 nickels and pennies below it). The value of a nickel is 5 cents.
Example Question #72 : Statistics
A student decides to review all of his old tests from his math class in order to prepare for the upcoming exam. The student decides that any exam in which he received a 94% or better he should be able to skip since he understood the material well, but he will review the rest. The first 7 tests are scored out of 50 points. The rest are scored out of 40 points. In order, they got the following raw scores:
The student has 1 more test to add to this list. If he puts together all the tests he must review in order of percentile score, this final test is the median score. Which of the following cannot be the raw score of this final test?
We first remove any 94%+ scores. For tests scored out of 50, a 94% is a 47. Thus anything 47 or greater will be removed. We see that this leaves us with:
For the second half, we have tests scored out of 40. 94% of 40 gives us 37.6, thus we will only remove tests that were a 38 or better. This leaves us with:
Now we have to convert them to percentiles. We end up with the lists as follows. The raw scores are in parentheses:
We then order it by percentile (removing raw scores, as they are unnecessary):
We notice that the median must be between the 78 and the 87.5 percentile scores. 31 out of 40 gives us 77.5%, which is below the score associated with an earlier test. Thus this cannot be the answer. The remaining 4 scores are all higher than 78%, and the largest of them is equal to 87.5 (the highest bound).
Example Question #11 : Median
67, 73, 85, 83, 80, 73, 94, 65, 80, 73, 98, 59, 76
The list above shows a ninth grader's grades for the academic year. What is the difference between the median and the mode of these grades?
To find the median, sort the numbers from smallest to largest:
59, 65, 67, 73, 73, 73, 76, 80, 80, 83, 85, 94, 98
The median is the middle value in a list of numbers, it is the number separating the higher half of a data sample or a list of numbers from the lower half.
The median of the grades is 76.
The mode is the value occurring most often. The most occurring value in the list of numbers given is 73. So, the mode is 73.
Example Question #11 : Median
What is the median for the following test scores of students on a test:
In order to solve this problem, the tests need to be organized from smallest to largest.
The median is the middle number in the set of data. From here the smallest and the largest numbers can be "crossed off" until one number remains. This gives the correct answer of 88.
Certified Tutor
All SAT Math Resources