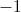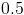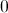All Precalculus Resources
Example Questions
Example Question #1 : Hyperbolas
Using the information below, determine the equation of the hyperbola.
Foci: 
Eccentricity:
General Information for Hyperbola:
Equation for horizontal transverse hyperbola:
Distance between foci =
Distance between vertices =
Eccentricity =
Center: (h, k)
First determine the value of c. Since we know the distance between the two foci is 12, we can set that equal to 
Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.
Eccentricity =
Determine the value of
Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 4, the center point will be on the same line. Hence, 
Since center point is equal distance from both foci, and we know that the distance between the foci is 12, we can conclude that
Center point:
Thus, the equation of the hyperbola is:
Example Question #2 : Hyperbolas
Using the information below, determine the equation of the hyperbola.
Foci: 
Eccentricity:
General Information for Hyperbola:
Equation for horizontal transverse hyperbola:
Distance between foci =
Distance between vertices =
Eccentricity =
Center: (h, k)
First determine the value of c. Since we know the distance between the two foci is 8, we can set that equal to 
Next, use the eccentricity equation and the value of the eccentricity provided in the question to determine the value of a.
Eccentricity =
Determine the value of
Determine the center point to identify the values of h and k. Since the y coordinate of the foci are 8, the center point will be on the same line. Hence, 
Since center point is equal distance from both foci, and we know that the distance between the foci is 8, we can conclude that
Center point:
Thus, the equation of the hyperbola is:
Example Question #1 : Finding Maxima And Minima
The function 
When you take the second derivative of the function 
What can you conclude about the function at 
The point is an inflection point.
The point is a local minimum.
The point is a local maximum.
The point is an absolute maximum.
The point is an absolute minimum.
The point is an inflection point.
We have a point at which 
Plug in 0 into the second derivative to obtain
So the point is an inflection point.
Example Question #3 : Pre Calculus
Consider the function
Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex)
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex)





Plugging in either 1 or 0 into the original function 
Example Question #1 : Introductory Calculus
In what 
A cubic function will have at most one relative minimum and one relative maximum. We can determine the zeros be factoring at 
The graph is positive between 




Example Question #15 : Pre Calculus
What is the minimum of the function 
The vertex form of a parabola is:
where 
The function for this problem can be simplified into vetex form of a parabola:

with a vertex at 
Since the parabola is concave up, the minimum will be at the vertex of the parabola, which is at 
Example Question #1 : Graphing Functions
What is the y-intercept of the following equation?
The y-intercept can by found by solving the equation when x=0. Thus,
Example Question #2 : Graphing Functions
Determine the y intercept of 

In order to determine the y-intercept of 
Solving for y, when x is equal to zero provides you with the y coordinate for the intercept. Thus the y-intercept is 
Example Question #2 : Graphing Functions
What is the 

To find the 


Substituting 
Therefore, our 

Example Question #3 : Graphing Functions
What is the value of the 

The graph does not have a 
To find the 



All Precalculus Resources