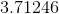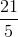Irrational Numbers
Help Questions
Pre-Algebra › Irrational Numbers
Which of the following is an irrational number?
Explanation
An irrational number is any number that cannot be written as a fraction of whole numbers. The number pi and square roots of non-perfect squares are examples of irrational numbers.






Which of the following is an irrational number?
Explanation
An irrational number is any number that can not be expressed as a ratio of integers, i.e. a fraction. Therefore, the only irrational number listed is 
Which of the following is closest to the value of the expression 
The expression is undefined in the real numbers.
Explanation
Since 

We can determine which is closer by evaluating 
Since 
Which of the following is an irrational number?
Explanation
A rational number can be expressed as a fraction of integers, while an irrational number cannot.




The number 


The number, 

Of the following, which is an irrational number?
Explanation
The definition of an irrational number is a number which cannot be expressed in a simple fraction, or a number that is not rational.
Using the above definition, we see that 




This is an irrational number and our correct answer.
Which of the following numbers is considered to be an irrational number?
Explanation
An irrational number cannot be represented as the quotient of two integers.
Irrational numbers do not terminate and are not repeat numbers.
Looking at the possible answers,








Which of the following is NOT an irrational number?
Explanation
Rational numbers are those which can be written as a ratio of two integers, or simply, as a fraction.
The solution of 


Of the following, which is a rational number?
Explanation
A rational number is any number that can be expressed as a fraction/ratio, with both the numerator and denominator being integers. The one limitation to this definition is that the denominator cannot be equal to 
Using the above definition, we see 






Which of the following expressions is irrational?
Explanation
An irrational number is defined as any number that cannot be expressed as a simple fraction or does not have terminating or repeating decimals. Of the answer choices given, the only number that cannot be expressed as a simple fraction or with repeating or terminating decimals is 
What do you get when you multiply two irrational numbers?
Sometimes irrational, sometimes rational.
Always rational.
Always irrational.
Integers.
Imaginary numbers.
Explanation
Let's take two irrationals like 

But what if we took the product of 


This makes it irrational and therefore, the answer is sometimes irrational, sometimes rational.