All MCAT Physical Resources
Example Questions
Example Question #1 : Work
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 30o. The coefficient of kinetic friction for the ramp is 0.1.
What is the work done by gravity on the box?
Work is determined using the equation 




Notice how the work done by gravity is equal to the potential energy of the box at the top of the ramp. This is because mechanical energy is conserved in the system; thus, we can set the two equations equal to each other.
Example Question #2 : Work, Energy, And Power
What is the work done on a 


Work is represented by the product of force and displacement:
We are given the force on the box and the distance it travels. Use these values to calculate the work done.
Note that the mass of the box for this problem is irrelevant. There is no vertical displacement, so the force of gravity does not come into play. The only force that matters in this question is the "pushing force."
Example Question #1 : Work, Energy, And Power
Two students (student X and student Y) lift a boulder vertically from point A to point B. Student X directly lifts the boulder from point A to point B, whereas student Y uses a pulley to lift the boulder. This allows student Y to apply a force (

The vertical distance between point A and point B is 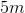
Student Z uses an inclined plane to lift the boulder and exerts only one third of 
the same because work is a state function in a gravitational field
different because work is a path function in a gravitational field
different because work is a state function in a gravitational field
the same because work is a path function in a gravitational field
the same because work is a state function in a gravitational field
Work is generally considered a path function. This means that the amount of work depends on the path taken.
Work in a gravitational field, however, is not a path function; it is a state function. This means that work is independent of the path taken in a gravitational field. This occurs because the force due to gravity acts only in one direction (downwards); therefore, the work performed with or against gravity will only depend on the vertical distance travelled.
In this question both students lift the boulder along the same vertical distance (a distance of 

Example Question #2 : Work, Energy, And Power
How much work is done to lift a 

The work done is equal to the gravitational potential energy of the block after it has been lifted.
The gravitational potential energy is calculated using the following formula:
We are given the mass and the change in height, and we know the acceleration due to gravity. Using these values, we can solve for the change in potential energy by multiplication.
Example Question #2 : Work, Energy, And Power
What is the work done by gravity if a 50kg block is pushed along a 40m track?
The work done by any force that is perpendicular to the displacement is equal to zero. Since the block is moving horizontally, the net force in the vertical direction will be equal to zero; therefore, work done by either gravity or the normal force will be equal to zero.
Example Question #3 : Work, Energy, And Power
An object of mass 100g moves in circular path of radius 0.5m, under the influence of a 15N force directed radially inwards towards the center of the path. How much work is done by this force as the object moves one quarter of the way around the circle?
4.8J
11.8J
47J
7.5J
0J
0J
Work is given by 

Example Question #1 : Work, Energy, And Power
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 30o. The coefficient of kinetic friction for the ramp is 0.1.
What is the work done by the normal force on the box?
Remember that the work done by a force on an object is dependent on the angle of the force to the object's displacement. The normal force acts perpendicularly to the ramp, which means it has an angle of 90o with respect to the box's displacement.
Because 

Example Question #5 : Work, Energy, And Power
A student carries a 

Since the height of the books is constant, there is no change in potential energy. Similarly, since the speed of the books is constant, there is no change in kinetic energy. By the work-energy theorem, work is equal to the change in mechanical energy (including potential and kinetic). If there is zero change in energy, the work done must also be zero.
We can also look at this problem in terms of forces. There is zero acceleration on the books, since they do not move in the vertical direction and the horizontal velocity is constant. If there is no acceleration, then there is no force. If there is no force, then there is no work, according to Newton's second law.
Example Question #1 : Work, Energy, And Power
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 

Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
Consider that child 1 adds 5kg of books to her backpack. She then prepares to slide down the ramp to the lake surface. If she slides down the ramp but stops herself after she has lost 2m in vertical height, how much work does the force of gravity perform on her to get her to her new position? Ignore assume the ramp is frictionless.
The amount of work performed to get child 1 down the ramp is equal to the amount of kinetic energy gained by her from top to bottom, via the work-energy theorem. Unfortunately, we are not given her kinetic energy. We can't use the 5m/s in the passage, because she stops herself before sliding to the lake surface.
We must instead recognize the potential energy lost is equal to kinetic energy gained. The potential energy that she has lost is given by mgh.
Example Question #1 : Work, Energy, And Power
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 

Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
Before collision 3 takes place, suppose that child 1 starts at the top of a ramp that is 3m long, and 
With what speed does child 1 hit the lake surface? Ignore friction and air resistance.
This is an application of the work-energy theorem. The amount of work done by the force of gravity to move child 1 down the ramp is equal to force * distance, as well as equal to the amount of kinetic energy picked up down the ramp.
The force down the ramp is equal to mg*sin(30o) = 600J * 0.5 = 300J
Certified Tutor
All MCAT Physical Resources




























































