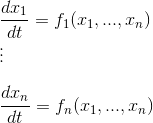Chaos and Fractals
Help Questions
Math Modeling › Chaos and Fractals
There are two similar species of monkey that inhabit the same forest. The intrinsic growth rate is 4% for species A and 7% for species B. The capacity of the forest is estimated at 125,000 specie A monkeys and 450,000 species B monkeys. Poaching these monkeys over the last 100 years has caused for a decline in each species. Species A has a population of 4,000 and species B, a population of 80,000. Use a discrete model to project the population growth with a time step of several years. How large a time step can be used to maintain a continuous time model with an equivalent qualitative behavior?
Assume 
Explanation
Identify the known information and the dynamical system.
The dynamical system equation is:
From here solve by using the Euler Method for a discrete time dynamical system.
Now formulate the model
Now transform these equations into a set of difference equations.
Assume
where 
The time step 
Using computer implementation of the Euler Method on the population of species B monkeys the following graph is produced.

It is seen that