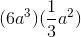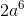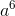Simplify the following expression:

To solve this question, we need to recall that when dividing exponents we subtract them.

When dividing coefficients, we treat them as regular division.

In this case, we can break up our question into two parts:

The coefficients will simply reduce to "2", because 16 divided by 8 is two

The r's are another story. We subtract, so we will get the following:

So, if we put our two parts back together, we get:

The correct answer is , and this can be determined in the following manner.

First, find the approximate square root of the number:

We know this because:

Therefore, we only need to consider prime numbers through

Is evenly divisible by any of these numbers? In this case, the answer is no, therefore is prime. Consider the case where the answer is not prime: .

We know this because:

Therefore, we need to consider the followig prime numbers:

Is divisible by any of these numbers? In this case, the answer is yes. is divisible by .

Based on the power rule, we know that in order to raise a power to a power we need to multiply the exponents, i.e.

.

Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:

So we can write:

in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get:

The correct answer is , and this can be determined in the following manner.

First, find the approximate square root of the number:

We know this because:

Therefore, we only need to consider prime numbers through

Is evenly divisible by any of these numbers? In this case, the answer is no, therefore is prime. Consider the case where the answer is not prime: .

We know this because:

Therefore, we need to consider the followig prime numbers:

Is divisible by any of these numbers? In this case, the answer is yes. is divisible by .

Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:

So we can write:

in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get:

Simplify the following expression:

To solve this question, we need to recall that when dividing exponents we subtract them.

When dividing coefficients, we treat them as regular division.

In this case, we can break up our question into two parts:

The coefficients will simply reduce to "2", because 16 divided by 8 is two

The r's are another story. We subtract, so we will get the following:

So, if we put our two parts back together, we get:

Based on the power rule, we know that in order to raise a power to a power we need to multiply the exponents, i.e.

.

Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:

So we can write:

Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:

So we can write:

in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get: