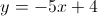All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #1 : Geometry
Give the equation of the line through point 

Use the point-slope formula with
Example Question #2 : How To Find A Line On A Coordinate Plane
Which is the greater quantity?
(A) The slope of the line
(B) The slope of the line
(B) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(A) is greater
(A) is greater
Rewrite each in the slope-intercept form, 

The slope of this line is 
The slope of this line is 
Since 
Example Question #2 : Geometry
Which is the greater quantity?
(A) The slope of the line
(B) The slope of the line
It is impossible to determine which is greater from the information given
(B) is greater
(A) and (B) are equal
(A) is greater
(A) and (B) are equal
Rewrite each in the slope-intercept form, 

The slope of the line of 
The slope of the line of 
The slopes are equal.
Example Question #4 : Coordinate Geometry



(a) The slope of the line on the coordinate plane through the points 

(b) The slope of the line on the coordinate plane through the points 

(a) and (b) are equal
It is impossible to determine which is greater from the information given
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
The slope of a line through the points 

in the slope formula:
The slope of a line through the points 

The lines have the same slope.
Example Question #2 : Geometry
A line passes through the points with coordinates 


Undefined
The slope of a line through the points 


in the slope formula:
Example Question #2 : Geometry
Choose the best answer from the four choices given.
The point (15, 6) is on which of the following lines?
For this problem, simply plug in the values for the point (15,6) into the different equations (15 for the 





Example Question #3 : Geometry
Choose the best answer from the four choices given.
What is the point of intersection for the following two lines?
At the intersection point of the two lines the 

point of intersection
Example Question #4 : Geometry
Choose the best answer from the four choices given.
What is the 
In the formula 



Thus, to find the 


Example Question #1 : Geometry
The ordered pair 
Quadrant I
Quadrant IV
Quadrant II
Quadrant V
Quadrant III
Quadrant II
There are four quadrants in the coordinate plane. Quadrant I is the top right, and they are numbered counter-clockwise. Since the x-coordinate is 

Example Question #2 : Geometry
If angles s and r add up to 180 degrees, which of the following best describes them?
Complementary
Supplementary.
Obtuse
Acute
Supplementary.
Two angles that are supplementary add up to 180 degrees. They cannot both be acute, nor can they both be obtuse. Therefore, "Supplementary" is the correct answer.
All ISEE Middle Level Quantitative Resources