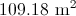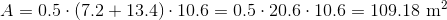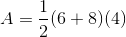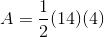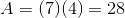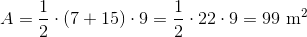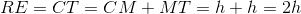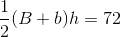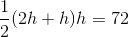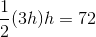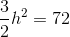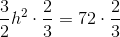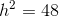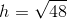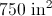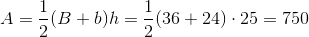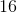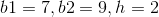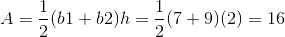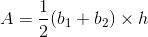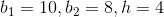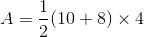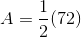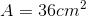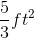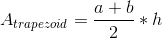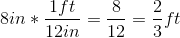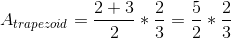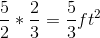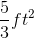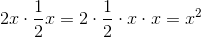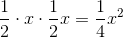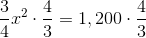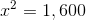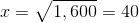All ISEE Middle Level Math Resources
Example Questions
Example Question #1 : How To Find The Area Of A Trapezoid
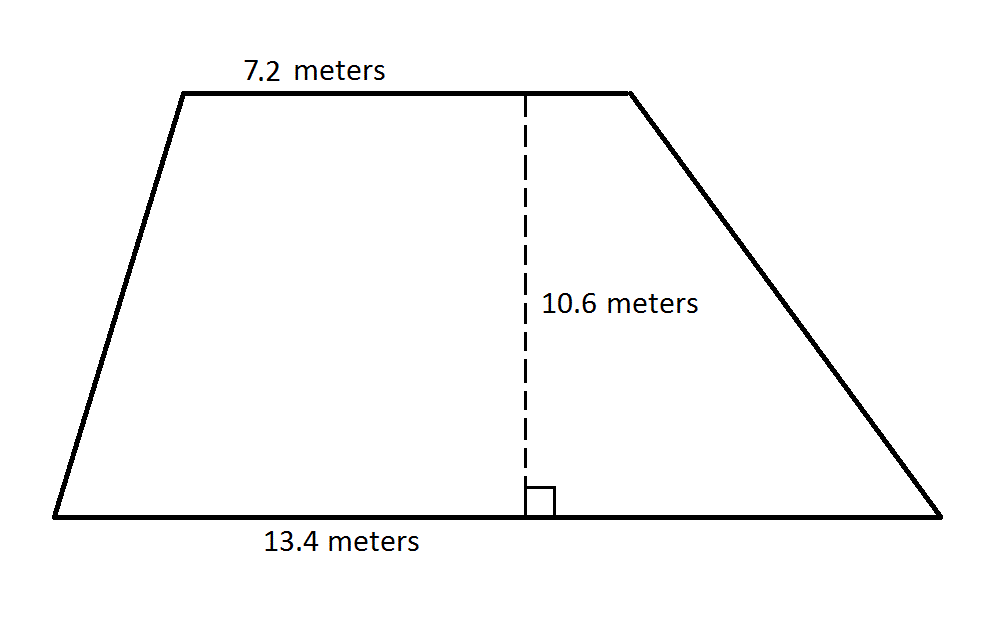
What is the area of the above trapezoid?
To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is
Example Question #251 : Geometry
Find the area of the trapezoid:
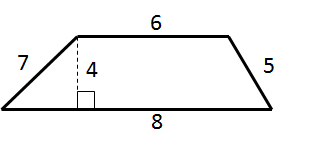
The area of a trapezoid can be determined using the equation 
Example Question #1 : How To Find The Area Of A Trapezoid
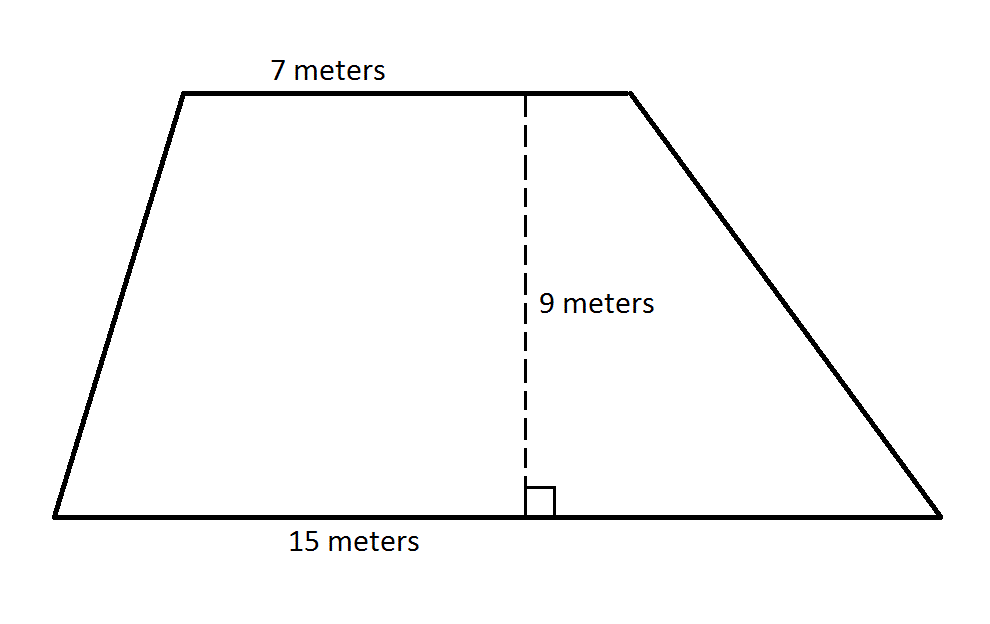
What is the area of the trapezoid?
To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.
Example Question #2 : How To Find The Area Of A Trapezoid
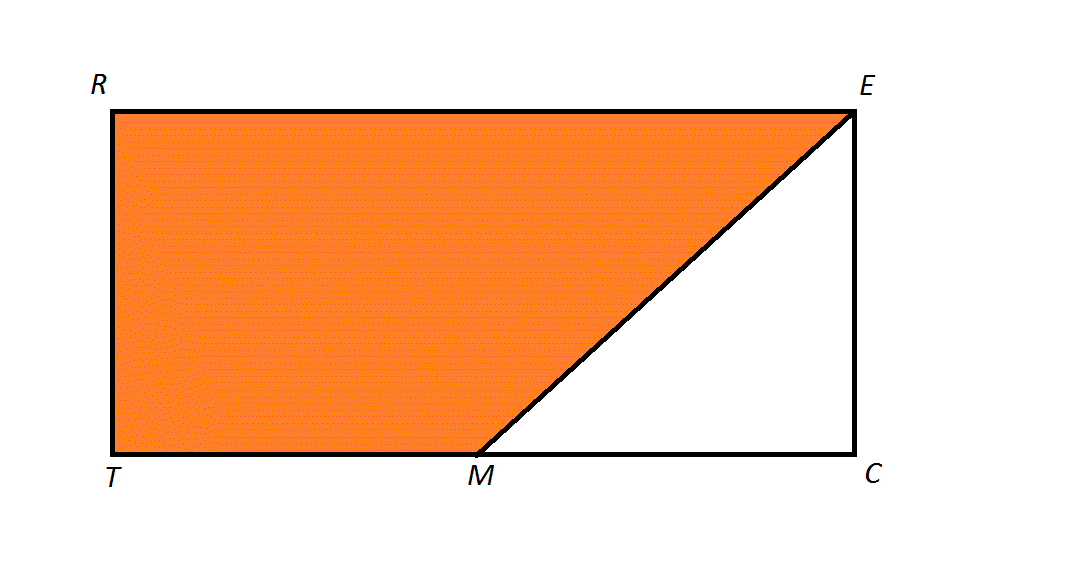
The above diagram depicts a rectangle 





The length of a leg of 

Since the triangle is isosceles, then 



Therefore, the orange region is a trapezoid with bases 


This is the length of one leg of the triangle.
Example Question #261 : Geometry
A trapezoid has a height of 


Use the following formula, with 
Example Question #261 : Plane Geometry
Find the area of a trapezoid with bases equal to 7 and 9 and height is 2.
To solve, simply use the formula for the area of a trapezoid.
Thus,
Example Question #1 : How To Find The Area Of A Trapezoid
Find the area of a trapezoid with bases of 10 centimeters and 8 centimeters, and a height of 4 centimeters.
The formula for area of a trapezoid is:
where
therefore the area equation becomes,
Example Question #6 : How To Find The Area Of A Trapezoid
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
Cannot be determined from the information provided.
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the depth is 8 inches, what is the area of the base of your new bookshelf?
To find the area of a trapezoid, we need to use the following formula:
Where a and b are the lengths of the bases, and h is the perpendicular distance from one base to another.
We are given a and b, and then h will be the same as our depth. The tricky part is realizing that our depth is in inches, while our base lengths are in feet. We need to convert 8 inches to feet:
Next, plug it all into our equation up above.
So our answer is:
Example Question #7 : How To Find The Area Of A Trapezoid
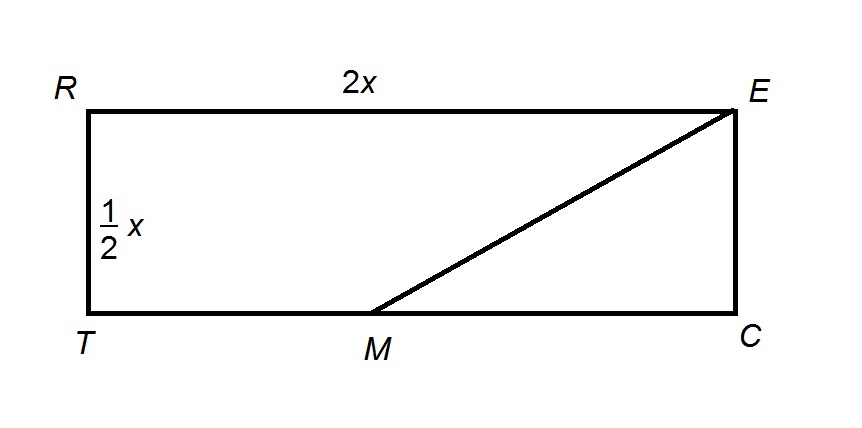
The above diagram shows Rectangle 


The area of Quadrilateral 


The easiest way to see this problem is to note that Quadrilateral 


The area of Rectangle 





its area is half their product, or
The area of Quadrilateral 

Example Question #112 : Geometry
The perimeter of the following trapezoid is equal to 23 cm. Solve for 
The perimeter is equal to the sum of all of the sides.
Certified Tutor
Certified Tutor
All ISEE Middle Level Math Resources