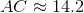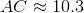Solving Triangles

Help Questions

Math › Solving Triangles

Questions 1 - 10

Hexagon

The above hexagon is regular. What is ?

None of the other responses is correct.

Explanation

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

$\frac{180^{\circ } (6-2)}{6}= 120^{\circ }$ .

The four angles of the quadrilateral are $120 ^{\circ }, 120^{\circ }, 41^{\circ }, x^{\circ }$ . Their sum is $360^{\circ }$ , so we can set up, and solve for in, the equation:

Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?

The triangle cannot exist.

The triangle is acute and equilateral.

The triangle is obtuse and isosceles, but not equilateral.

The triangle is acute and isosceles, but not equilateral.

The triangle is obtuse and scalene.

Explanation

One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,

That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.

If the angles and are supplementary, what must be the value of ?

$-\frac{37}{3}$

$\frac{37}{3}$

Explanation

Supplementary angles sum up to 180 degrees.

Add five on both sides.

Divide by negative five on both sides to determine .

$\frac{-5x}{-5} = \frac{185}{-5}$

The answer is:

Triangle

Note: figure NOT drawn to scale.

Refer to the triangle in the above diagram.

Evaluate . Round to the nearest tenth, if applicable.

$AC \approx 14.2$

$AC \approx 10.3$

$AC \approx 18.0$

$AC \approx 32.4$

$AC \approx 30.4$

Explanation

By the Law of Cosines,

$\left (AC \right )^{2} =\left (AB \right )^{2}+ \left (BC \right )^{2} - 2 (AB)(BC) \cos b^{\circ }$

Substitute :

$\left (AC \right )^{2} =15^{2}+20^{2} - 2 \cdot15 \cdot 20 \cos 45^{\circ }$

$\left (AC \right )^{2} =225+400 - 600 \cdot \frac{\sqrt{2}}{2}$

$\left (AC \right )^{2} \approx 625 -424.26$

$\left (AC \right )^{2} \approx 200.74$

$AC \approx \sqrt{200.74} \approx 14.2$

Decagon

The above figure is a regular decagon. Evaluate to the nearest tenth.

$x \approx 11.4$

$x \approx 10.8$

$x \approx 11.6$

$x \approx 9.7$

$x \approx 10.4$

Explanation

Two sides of the triangle formed measure 6 each; the included angle is one angle of the regular decagon, which measures

$m = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }$ .

Since we know two sides and the included angle of the triangle in the diagram, we can apply the Law of Cosines,

$c^{2}= a^{2}+ b^{2} - 2ab \cos C^{\circ }$

with and :

$x ^{2}= 6^{2} + 6^{2} - 2 \cdot 6 \cdot 6 \cos 144^{\circ }$

$x ^{2}= 36+ 36- 72 \cos 144^{\circ }$

$x ^{2} \approx 72 - 72 \left ( -0.8090\right )$

$x \approx 11.4$

Triangle

Note: figure NOT drawn to scale.

Refer to the triangle in the above diagram.

Evaluate . Round to the nearest tenth, if applicable.

$BC \approx 13.2$

$BC \approx 8.1$

$BC \approx 10.6$

$BC \approx 21.8$

$BC \approx 23.2$

Explanation

By the Law of Cosines,

$\left (BC \right )^{2} =\left (AB \right )^{2}+ \left (AC \right )^{2} - 2 (AB)(AC) \cos a^{\circ }$

Substitute :

$\left (BC \right )^{2} =15^{2}+10^{2} - 2 \cdot15 \cdot 10 \cos 60^{\circ }$

$\left (BC \right )^{2} =225+100 - 300 \cdot \frac{1}{2}$

$\left (BC \right )^{2} =225+100 - 150$

$\left (BC \right )^{2} = 175$

$BC = \sqrt{175} \approx 13.2$

Pentagon

The above figure is a regular pentagon. Evaluate to the nearest tenth.

$x \approx 6.5$

$x \approx 6.1$

$x \approx 6.9$

$x \approx 5.7$

$x \approx 5.4$

Explanation

Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures

$m = \left [\frac{180(5-2)}{5} \right ] ^{\circ }= 108^{\circ }$

The length of the third side can be found by applying the Law of Cosines:

$x^{2} = a^{2} + b^{2} - 2ab \cos C^{\circ }$

where :

$x^{2} = 4^{2} + 4^{2} - 2 \cdot 4 \cdot 4 \cos 108^{\circ }$

$x^{2} = 16 +16 -32 \cos 108^{\circ }$

$x^{2} \approx 32 -32 \left ( -0.3090\right )$

$x^{2} \approx 41.88$

$x \approx \sqrt{41.88} \approx 6.5$

If a set of angles are supplementary, what must be the other angle if a given angle is ?

$145^\circ$

$215^\circ$

$155^\circ$

$135^\circ$

$55^\circ$

Explanation

Supplementary angles must add up to 180 degrees.

To find the missing angle, subtract the known angle from 180 degrees.

The answer is: $145^\circ$

Regular Pentagon has perimeter 60.

To the nearest tenth, give the length of diagonal $\overline{BD}$ .

Explanation

The perimeter of the regular pentagon is 60, so each side measures one fifth of this, or 12. Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

The pentagon, along with diagonal $\overline{BD}$ , is shown below:

Pentagon 2

A triangle $\bigtriangleup BCD$ is formed with , and included angle measure $\angle B= 108^{\circ }$ . The length of the remaining side can be calculated using the Law of Cosines: