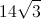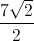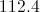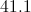All High School Math Resources
Example Questions
Example Question #1 : Triangles
 In this figure, side
In this figure, side 



Undefined
Since 
That means that 
In this problem, that would be:
Plug in our given values:
Example Question #1 : Applying Trigonometric Functions
Let ABC be a right triangle with sides 






We are looking for 

So therefore, without figuring out 
Example Question #1 : Trigonometric Functions And Graphs

In this figure, if angle 



Undefined
Since 
That means that 
In this problem, that would be:
Plug in our given values:
Example Question #85 : Trigonometry

In this figure, 



Undefined
Notice that these sides fit the pattern of a 30:60:90 right triangle: 
In this case, 
Since angle 


Example Question #86 : Trigonometry
A triangle has angles of 



The pattern for 

If the side opposite 



Example Question #2 : Triangles
In 




A triangle with these sidelengths cannot exist.
By the Triangle Inequality, this triangle can exist, since 
By the Law of Cosines:
Substitute the sidelengths and solve for 
Example Question #3 : Triangles
A triangle has sides of length 12, 17, and 22. Of the measures of the three interior angles, which is the greatest of the three?
We can apply the Law of Cosines to find the measure of this angle, which we will call :
The widest angle will be opposite the side of length 22, so we will set:


Example Question #61 : Pre Calculus
In 




A triangle with these characteristics cannot exist.
By the Law of Cosines:
or, equivalently,
Substitute:
Example Question #4 : Triangles

In this figure, angle 



For this problem, use the law of sines:

In this case, we have values that we can plug in:
Cross multiply:
Multiply both sides by 
Example Question #5 : Triangles

In this figure 



For this problem, use the law of sines:

In this case, we have values that we can plug in:
All High School Math Resources