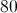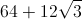All High School Math Resources
Example Questions
Example Question #1 : Parallelograms
A parallelogram, with dimensions in cm, is shown below.
What is the perimeter of the parallelogram, in cm?
The triangle on the left side of the figure has a 


Our third angle is 

A 



We also now know that
Now we know all of our missing side lengths. The right and left side of the parallelogram will each be 

Example Question #2 : Parallelograms
Find the perimeter of the following parallelogram:

The formula for the perimeter of a trapezoid is:

where 

Opposite sides of a parallelogram have the same length. Therefore, both edges are 

Plugging in our values, we get:
Example Question #172 : Plane Geometry
Find the perimeter of the following parallelogram:

The formula for the perimeter of a parallelogram is:
where 

Plugging in our values, we get:
Example Question #4 : Parallelograms
Find the perimeter of the following parallelogram:

The formula for the perimeter of a parallelogram is

Plugging in our values, we get:
Example Question #173 : Plane Geometry
ABCD is a parallelogram. BD = 5. The angles of triangle ABD are all equal. What is the perimeter of the parallelogram?
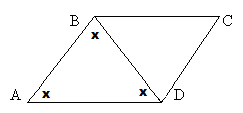
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.
We now have two equilateral triangles, so all sides of the triangles will be equal.
All sides therefore equal 5.
5+5+5+5 = 20
Example Question #1 : Parallelograms
In the parallellogram, what is the value of 

Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2z = x = 130°
Example Question #1 : Parallelograms
What is the area of a parallelogram with a base of 

To solve this question you must know the formula for the area of a parallelogram.
In this equation, 

Example Question #5 : Parallelograms
What is the area of a parallelogram with a base of 

To solve this question you must know the formula for the area of a parallelogram.
The formula is
So we can plug in the side length for both base and height to yield
Perform the multiplication to arrive at the answer of 
Example Question #9 : Parallelograms
Find the area of the following parallelogram:

Cannot be determined from the given information.
The formula for the area of a parallelogram is:

where 

In order to the find the height of the parallelogram, use the formula for a 



The left side of the parallelogram forms the following 


Plugging in our values, we get:
Example Question #1 : How To Find The Area Of A Parallelogram
Find the area of the following parallelogram:

Use the Pythagorean Theorem to determine the length of the diagonal:
The area of the parallelogram is twice the area of the right triangles:
Certified Tutor
All High School Math Resources