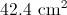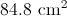High School Math

Help Questions

Math › High School Math

Questions 1 - 10

To the nearest tenth, give the area of a $60^{\circ }$ sector of a circle with diameter 18 centimeters.

$42.4 \textrm{ cm}^{2}$

$84.8 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$

Explanation

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

If we know the lengths of sides , , and , then we can simply add them together to find the perimeter of the triangle. It is important to note several things. First, we need to make sure that all the units given match one another. Second, when all the side lengths are known, then the perimeter formula may be used on all types of triangles (e.g. right, acute, obtuse, equilateral, isosceles, and scalene). The perimeter formula is written formally in the following format:

$\textup{Perimeter}=a+b+c$

Method 2:

In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one $90^{\circ}$ angle. It is a special triangle and needs to be labeled accordingly. The legs of the triangle form the $90^{\circ}$ angle and they are labeled and . The side of the triangle that is opposite of the $90^{\circ}$ angle and connects the two legs is known as the hypotenuse. The hypotenuse is the longest side of the triangle and is labeled as .

Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

Screen shot 2016 07 07 at 12.58.14 pm

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

Recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

The given triangle has of the three sides needed. Use the Pythagorean theorem to find the length of the third side.

Recall the Pythagorean theorem:

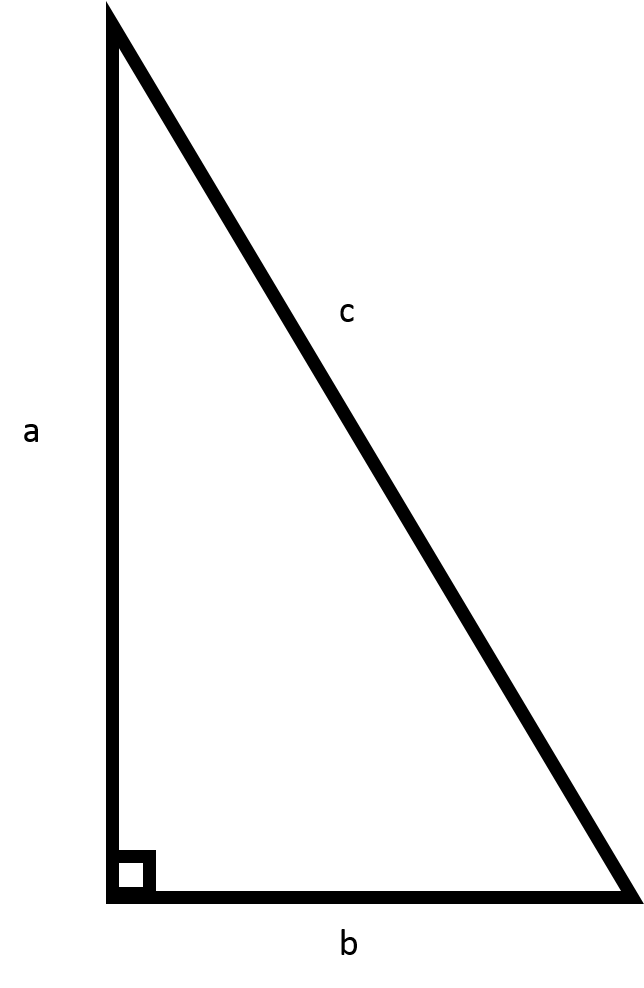
Since we are finding the length of side , rewrite the equation.

$b=\sqrt{c^2-a^2}$

Plug in the values of and .

$b=\sqrt{25^2-16^2}=\sqrt{369}$

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to decimal places.

$\text{Perimeter}=25+16+\sqrt{369}=60.21$

Calculate the perimeter of the polygon.

Explanation

The perimeter is the sum of the length of all of the sides. We are given all of the side lengths in the figure, so we simply need to sum them together.

The area of a rectangle is . How many whole by rectangles can fit inside of this larger rectangle?

$13\tfrac{1}{3}$

Explanation

First we need to find the area of the smaller rectangle.

Now to find out how many can fit, we divide the total area by the smaller area.

$\frac{200ft^2}{15ft^2}=x$

$13\tfrac{1}{3}=x$

However, the problem is asking how many WHOLE rectangles can fit. Therefore only can fit.

If the diagonal of a square is $19\sqrt2$ , what is the area of the square?

Explanation

The diagonal of a square is also the hypotenuse of a triangle whose legs are the sides of the square.

Thus, from knowing the length of the diagonal, we can use Pythagorean's Theorem to figure out the side lengths of the square.

$\text{Diagonal}^2=\text{side length}^2+\text{side length}^2$

$\text{Diagonal}^2=2(\text{side length})^2$

$(\text{side length})^2=\frac{\text{Diagonal}^2}{2}$

$\text{side length}=\frac{\text{Diagonal}}{\sqrt2}$

We can now find the side length of the square in question.

$\text{side length}=\frac{19\sqrt2}{\sqrt2}$

Simplify.

$\text{side length}=19$

Now, recall how to find the area of a square:

$\text{Area}=(\text{side length})^2$

For the square in question,

$\text{Area }=19 ^2$

Solve.

$\text{Area }=361$

Find the perimeter.

Explanation

How do you find the perimeter of a right triangle?

There are three primary methods used to find the perimeter of a right triangle.

When side lengths are given, add them together.
Solve for a missing side using the Pythagorean theorem.
If we know side-angle-side information, solve for the missing side using the Law of Cosines.

Method 1:

This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

Screen shot 2016 07 07 at 11.31.44 am

$\textup{Perimeter}=a+b+c$

Method 2:

Screen shot 2016 07 07 at 10.13.54 am

If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:

We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, .

Rearrange and take the square root of both sides.

$\sqrt{c^2}=\sqrt{a^2+b^2}$

Simplify.

$c=\sqrt{a^2+b^2}$

Now, let's use the Pythagorean theorem to solve for one of the legs, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{a^2}=\sqrt{c^2-b^2}$

Simplify.

$a=\sqrt{c^2-b^2}$

Last, let's use the Pythagorean theorem to solve for the adjacent leg, .

Subtract from both sides of the equation.

Take the square root of both sides.

$\sqrt{b^2}=\sqrt{c^2-a^2}$

Simplify.

$b=\sqrt{c^2-a^2}$

It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:

$c=\sqrt{a^2+b^2}$

$a=\sqrt{c^2-b^2}$

$b=\sqrt{c^2-a^2}$

After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.

Method 3:

Screen shot 2016 07 07 at 12.58.14 pm

$a^2=b^2+c^2-2bc\cdot \cos A$

$b^2=a^2+c^2-2ac\cdot \cos B$

$c^2=a^2+b^2-2ab\cdot \cos C$

Solution:

Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

Recall how to find the perimeter of a triangle:

$\text{Perimeter}=a+b+c$

The given triangle has of the three sides needed. Use the Pythagorean theorem to find the length of the third side.

Recall the Pythagorean theorem:

Since we are finding the length of the hypotenuse, , rewrite the equation.

$c=\sqrt{a^2+b^2}$

Plug in the values of and .

$c=\sqrt{5^2+9^2}=\sqrt{106}$

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to decimal places.

$\text{Perimeter}=5+9+\sqrt{106}=24.30$

In a certain quadrilateral, three of the angles are $65^{\circ}$ , $120^{\circ}$ , and $34^{\circ}$ . What is the measure of the fourth angle?

$141^{\circ}$

$139^{\circ}$

$219^{\circ}$

$41^{\circ}$

$29^{\circ}$

Explanation

A quadrilateral has four angles totalling $360^{\circ}$ . So, first add up the three angles given. The sum is $219^{\circ}$ . Then, subtract that from 360. This gives you the missing angle, which is $141^{\circ}$ .

What is the perimeter of a square with a side length of ?

Explanation

To find the perimeter of a square you must multiply the side length by .

To do this we plug the side length, , into the equation

Then multiply the side length by ,

The answer is .

Find the center and radius of the circle defined by the equation:

$\left ( 3,-5 \right )\ and\ r=6$

$\left ( 3,5 \right )\ and\ r=6$

$\left ( -3,-5 \right )\ and\ r=18$

$\left ( -3,5 \right )\ and\ r=18$

$\left ( -3,5 \right )\ and\ r=6$

Explanation

The equation of a circle is: $(x-x_{1})^2+(y-y_{1})^2=r^2$ where is the radius and $(x_{1},y_{1})$ is the center.

In this problem, the equation is already in the format required to determine center and radius. To find the -coordinate of the center, we must find the value of that makes equal to 0, which is 3. We do the same to find the y-coordinate of the center and find that . To find the radius we take the square root of the constant on the right side of the equation which is 6.