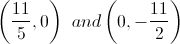Linear Functions
Help Questions
Math › Linear Functions
Solve:
No solutions
Infinitely many solutions
Explanation
Use substution to solve this problem:







Determine where the graphs of the following equations will intersect.
Explanation
We can solve the system of equations using the substitution method.
Solve for 
Substitute this value of 
Now we can solve for 
Solve for 

The solution is the ordered pair 
Determine where the graphs of the following equations will intersect.
Explanation
We can solve the system of equations using the substitution method.
Solve for 
Substitute this value of 
Now we can solve for 
Solve for 

The solution is the ordered pair 
Determine where the graphs of the following equations will intersect.
Explanation
We can solve the system of equations using the substitution method.
Solve for 
Substitute this value of 
Now we can solve for 
Solve for 

The solution is the ordered pair 
Shift the graph 
Explanation
Rewrite this equation in slope intercept form 
Add 
The equation becomes:
Divide by two on both sides.
The equation in slope intercept form is:
Shifting this equation down four units means that the y-intercept will be decreased four units.
The answer is:
Shift the graph 
Explanation
Rewrite this equation in slope intercept form 
Add 
The equation becomes:
Divide by two on both sides.
The equation in slope intercept form is:
Shifting this equation down four units means that the y-intercept will be decreased four units.
The answer is:
Which of the following is a horizontal line?
Explanation
A horizontal line has infinitely many values for 





Which of the following is a horizontal line?
Explanation
A horizontal line has infinitely many values for 





Solve for the 

Explanation
To solve for the 


To solve for the 


Which of the following is an equation of a vertical line?
Explanation
Think about the meaning of a vertical line on the coordinate grid. The