Chords
Help Questions
GMAT Quantitative › Chords
The chord of a 

Explanation
The radius 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

The arc 



Explanation
The figure referenced is below.
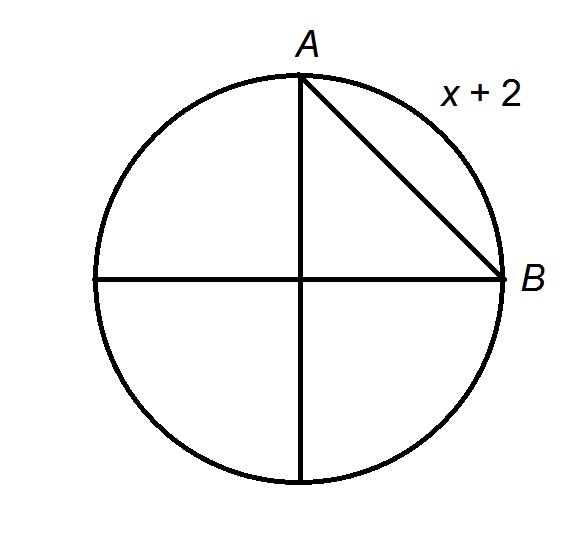
The arc is 

The radius is this circumference divided by 

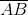


Calculate the length of a chord in a circle with a radius of 

Explanation
We are given the radius of the circle and the perpendicular distance from its center to the chord, which is all we need to calculate the length of the chord. Using the formula for chord length that involves these two quantities, we find the solution as follows, where 


Calculate the length of a chord in a circle with a radius of 

Explanation
We are given the radius of the circle and the perpendicular distance from its center to the chord, which is all we need to calculate the length of the chord. Using the formula for chord length that involves these two quantities, we find the solution as follows, where 


The chord of a 

Explanation
The radius 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

The arc 



Explanation
The figure referenced is below.

The arc is 

The radius is this circumference divided by 

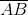


The chord of a 

Explanation
A circle with circumference 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

The chord of a 

Explanation
A circle with circumference 

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, 

Consider the Circle 

(Figure not drawn to scale.)
If 


Explanation
This is a triangle question in disguise. We have a ninety-degree triangle with two sides made up of the radii of the circle. This means the other two angles (


Use the 45/45/90 triangle ratios to find the final side. Additionally, you could use Pythagorean Theorem to find the missing side.
45/45/90 side length ratios:
Segment
Or, using the Pythagorean Theorem, 


The chord of a 

Explanation
The radius 

The circle, the central angle, and the chord are shown below, along with 

We concentrate on 
and
The chord 















































