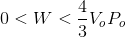Isothermal Processes
Help Questions
Physics › Isothermal Processes
Suppose that a piston contains a gas which begins at a certain pressure and volume. First, the gas in the piston undergoes an isothermal expansion to triple its initial volume. Next, the gas undergoes an isobaric contraction back to its original volume. Finally, the gas undergoes an isochoric increase in pressure until it has returned to its original pressure. Which of the following is a true statement regarding the work done by this gas?
Explanation
In this question, we're told the process that a gas takes through various changes in conditions. From this information, we're asked to find a true statement regarding the work done by the gas in this process.
At its initial point, we can define the gas as having an initial pressure and volume as 
First, we're told that the gas goes through an isothermal expansion to triple its volume. Recall that an isothermal process is one in which the temperature of the gas doesn't change. Moreover, because we're dealing with an ideal gas, we can see from the ideal gas equation that a constant temperature means that a changing volume must by accompanied by a change in pressure. Since the volume is being increased by a factor of three, we know that the pressure must be decreasing by a factor of three. Thus, right after the isothermal expansion has finished, the gas will have a pressure and volume of 
Next, we're told that the gas undergoes an isobaric contraction back to its original volume. Thus, we know from this that the pressure won't change, but the volume will return to its original value. Consequently, once the isobaric contraction has come to completion, the gas will have a pressure and volume of 
Finally, we're told that the last process is an isochoric increase of the pressure back to its original amount. Isochoric means that the volume doesn't change in this process. Hence, the gas will now be returned to its original pressure and volume of 
If we were to show this on a pressure vs. volume curve, it would look like the following.

Remember that any pressure-volume work done by a gas is the area under the curve of a pressure vs. volume diagram. For a cyclic process, as the one in this problem, the work done by the gas will be the area within the above image.
For this problem, we don't need to calculate the exact amount of work done. Instead, we can get a rough estimate by first realizing that the structure shown in the above diagram is close to forming a right triangle, but it is slightly smaller. Thus, if we can use the left and bottom sides of the image above to calculate the area that would be enclosed by a right triangle, we can infer that the work done in this problem will be slightly less than the calculated area.
The area for a triangle is the following.
So, for the image shown above, the bottom length is 

Finally, since this represents the area for a right triangle, we know that the actual work done is less than this. Hence, the correct answer is:
An ideal gas with an initial pressure of 


Explanation
We know that with the ideal gas law that:
We also know with isothermal processes, that the work done on a gas is:
Since the number of moles and the temperature is not given to us in the question, we can make a substitution with the ideal gas law to get:
Now we can plug in our known values into the equation to solve for the amount of work energy transferred through the isothermal process.