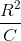Understanding Capacitors
Help Questions
AP Physics 1 › Understanding Capacitors
A capacitor has a stored charge of 

Explanation
To solve this problem, you need to use the following two equations:
By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.
Rearranging the previous equation will allow us to solve for the voltage.
Use the given values for stored potential energy and charge to solve for the voltage.
Which of the following is equal to the time constant of an RC circuit?
Explanation
The definition of a time constant for an RC circuit is the product of resistance and charge:
This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
I and III
I only
III only
II and III
Explanation
Recall the equation for potential energy in terms of capacitance:
According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:
In this equation,