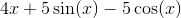All AP Calculus AB Resources
Example Questions
Example Question #1 : Interpretation Of The Derivative As A Rate Of Change
Find the rate of change of y if
The rate of change of y is also the derivative of y.
Differentiate the function given.
You should get
Example Question #22 : Applications Of Derivatives
If p(t) gives the position of an asteroid as a function of time, find the function which models the velocity of the asteroid as a function of time.
If p(t) gives the position of an asteroid as a function of time, find the function which models the velocity of the asteroid as a function of time.
Begin by recalling that velocity is the first derivative of position. So all we need to do is find the first derivative of our position function.
Recall that the derivative of sine is cosine, and that the derivative of polynomials can be found by multiplying each term by its exponent, and decreasing the exponent by 1.
Starting with:
We get:
Example Question #23 : Applications Of Derivatives
Given j(k), find the rate of change when k=5.
Given j(k), find the rate of change when k=5
Let's begin by realizing that a rate of change refers to a derivative.
So, we need to find the derivative of j(k)
We find this by multiplying each term by the exponent, and decreasing the exponent by 1
Next, plug in 5 to find our answer:
So, our rate of change is -221.
Example Question #4 : Interpretation Of The Derivative As A Rate Of Change
If p(t) gives the position of a planet as a function of time, find the function which models the planet's velocity.
If p(t) gives the position of a planet as a function of time, find the function which models the planet's velocity.
Velocity is the first derivative of position.
Therefore, all we need to do to solve this problem is to find the first derivative.
We can do this via the power rule and the rule for differentiating sine.
1)
2)
So, we these rules in mind, we get:
So our final answer is:
Example Question #5 : Interpretation Of The Derivative As A Rate Of Change
If p(t) gives the position of a planet as a function of time, find the planet's velocity when t=0.
If p(t) gives the position of a planet as a function of time, find the planet's velocity when t=0.
Velocity is the first derivative of position. Therefore, all we need to do to solve this problem is to find the first derivative of p(t) and then plug in 0 for t and solve.
We can do this via the power rule and the rule for differentiating sine and cosine.
1)
2)
So, we these rules in mind, we get:
So our velocity function is:
Now, plug in 0 and simplify.
So, our answer is -11. We are not given any units, so we do not need to worry about them.
Example Question #561 : Derivatives
A factory producing pens wants to maximize its output; to do so, it needs to find the rate of change of pen production. Find this rate if pens are produced according to the following function:
The rate of change of a function is given by the derivative of that function. So, to find the rate of change of production, we must take the first derivative of the function for production, which is equal to
found using the following rules:

Example Question #562 : Derivatives
Concrete at a factory flows according to the following theoretical model:
What is the rate of change of the concrete flow?
The rate of change of the concrete flow is given by the first derivative of the concrete flow function:
and was found using the following rules:


Example Question #563 : Derivatives
Find the speed of the car at t=5 if its position is given by
To determine the speed of the car, we must take the first derivative of the position function, which gives us the rate of change of the position of the car - in other words, speed.
The derivative was found using the following rule:

Evaluating the derivative function at t=5, we get our speed as
Example Question #31 : Applications Of Derivatives
A group of scientists use the following code for describing velocity and acceleration of particles:




What code - at t=2 - will the scientists use when describing a particle moving with a position function given by the following equation:
We need more information to determine the code used
To determine which code the scientists will use, we must find the velocity and acceleration of the particle, given by the first and second derivatives of the position function, respectively, evaluated at the given point.
The velocity and acceleration functions, therefore, are
The derivatives were found using the following rules:

Evaluated at t=2, we find that
When the velocity is positive, but the acceleration is negative, the code the scientists use is 
Example Question #564 : Derivatives
Find the velocity of the particle at x=0, its position given by the following function:
To determine the velocity of the particle, we must take the first derivative of the position function - in other words, the rate of change of the position is the velocity:
The derivative was found using the following rule:
To find the velocity at the given point, we simply plug in the value into the velocity function:
All AP Calculus AB Resources