All Algebra II Resources
Example Questions
Example Question #1 : Mean, Standard Deviation, And Normal Distribution
The mean of the following numbers is 13. Solve for x.
18, 15, 10, 8, x
15
13
14
12
14
where n equals the number of events.
Example Question #2 : Mean, Standard Deviation, And Normal Distribution
On 3 exams, Willow has an average score of 95 points. Her lowest score was an 90. If this score is dropped, what is her new average?
96
97.5
100
98
97.5
To answer this question, you must first calculate Willow's total points from the 3 exams. The total points will be equal to 3 times the original average:
95*3=285
Now, if the 90 is removed, his new total will be:
285-90=195
With the score dropped, her new total number of exams is 2. Therefore, the new average is:
Example Question #91 : Probability
The ages of the students at Rosa Parks High School are normally distributed with a mean of 15.5 and a standard deviation of 0.6 years.
What is the proportion of students that are older than 16.2 years old?
5%
1%
0%
2.5%
2.5%
This question relates to the 68−95−99.7 rule of normal distribution. We know that 95% of the data are within 2 standard deviations from the mean.
In this case this means that 95% of the students are between
15.5−2⋅0.6 and 15.5+2⋅0.5
15−1.2 and 15+1.2
13.8 and 16.2
Therefore we have 5% of the students that are outside of this range. Since the normal distribution is symmetric, the proportion of students below 13.8 is the same as the proportion of students above 16.2.
Thus the right answer is one half of 5%, or 2.5%.
2.5% of the students are older than 16.2 years old.
Example Question #4 : Mean, Standard Deviation, And Normal Distribution
The ages of the students at Central Universityl are normally distributed with a mean of 23.5 and a standard deviation of 2.5 years.
What is the proportion of students that are younger than 18.5 years old?
1%
5%
0%
2.5%
2.5%
This question relates to the 68−95−99.7 rule of normal distribution. We know that 95% of the data are within 2 standard deviations from the mean.
In this case this means that 95% of the students are between
23.5−2⋅2.5 and 23.5+2⋅2.5
23.5-5 and 23.5+5
18.5 and 28.5
Therefore we have 5% of the students that are outside of this range. Since the normal distribution is symmetric, the proportion of students below 18.5 is the same as the proportion of students above 28.5.
Thus the right answer is half of 5% or 2.5%.
Example Question #1 : Mean, Standard Deviation, And Normal Distribution
Find the standard deviation of the following set of numbers:
To begin, we must remember the formula for standard deviation:
where 


Now we can determine the value for our summation for each number in the set:
Looking at our equation for standard variation, now all we must do is sum all of the values above, divide by N, and take the square root:
Example Question #1 : Mean, Standard Deviation, And Normal Distribution
The formula for standard deviation is the following:

Where,

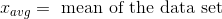
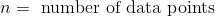
Five students took a test and recieved the following grades: 




None of the other answers.
The first step in solving for standrd deviation is to find the mean of the data set.
For this problem:

Now we can evaluate the summation:
Now we can rewrite the standard deviation expression:
There are 5 data points, so n = 5
Example Question #101 : Probability
In a normal distribution, what percentage is covered within one standard deviation?
34%
68%
99.7%
50%
95%
68%
By drawing a bell curve, the middle line is 50%. One standard deviation left and right of the middle line is 34% each. That means one standard deviation within is 68%.
Example Question #3 : Mean, Standard Deviation, And Normal Distribution
If the mean is 

Two standard deviations means to double the standard deviation value.
This means the range is 

Only 
Example Question #1 : Mean, Standard Deviation, And Normal Distribution
Ibram was paid $5000 for editing a 2200-page encyclopedia. What was his rate earned per page?
$2.27
$0.44
$1.27
$0.56
$2.27
This question is really just asking for the average dollar per page. This could be easily calculated:
However, you might also think of this as a rate problem:
D=RT
Using the information from the question, we can see that D=5000 and T=2200.
This comes out to what we solved above:
Example Question #1 : Mean, Standard Deviation, And Normal Distribution
Standard Deviation can be calculated from what statistical term?
Range
Variance
Quartile
Median
Mode
Variance
Another way to calculate standard deviation is the square root of variance.
Variance is,

Taking the square root of this is how standard deviation can be calculated.
Certified Tutor
All Algebra II Resources











































