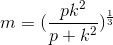How to find the solution to a rational equation with LCD
Help Questions
ACT Math › How to find the solution to a rational equation with LCD
bm/(_m_2 + 1)
–bm/(_m_2 + 1)
–b/(m + 1)
–b/(_m_2 – 1)
b/(_m_2 + 1)
Explanation
What is the slope of a line represented by the equation:
Explanation
To solve problems where you need to find the slope of a line in a given equation, change the equation so that it matches y-intercept form:
For this equation, first move the 3x over to the other side of the equation.

The equation should now look like this:
Then, divide by 15 to isolate the variable 
Then simplify
Whatever number is before the x in the equation (m) is your slope.
In the equation below, 





Explanation
John, Jill, and Jack are splitting a pizza. John eats 

Explanation
We can write an equation for the amount of pizza eaten, with 
To solve this equation, we must find the lowest common denominator of 



We can see that the least common multiple of 



When we put these fractions back into the equation, we can solve for 
–2
–1
0
1
2