All ACT Math Resources
Example Questions
Example Question #12 : Pentagons
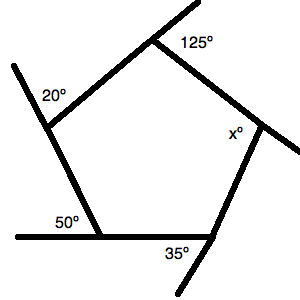
The figure above is a pentagon. All of the angles listed (except the interior one) are exterior angles to the pentagon's interior angles.
What is the value of 
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
Solve for 
Example Question #32 : Act Math

The figure above is a pentagon. All of the angles listed (except the interior one) are exterior angles to the pentagon's interior angles.
What is the value of the largest unknown angle in the figure above?
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
Solve for 
Now, you have to find the largest unknown angle, which is 
Example Question #33 : Act Math
What is the sum of three angles in a pentagon?
The sum of all angles is determined by the following formula for a polygon:
In a pentagon, there are 5 sides, or 
There are 5 interior angles in a pentagon. Divide the total possible angle by 5 to determine the value of one interior angle.
Each interior angle of a pentagon is 108 degrees.
The sum of three angles in a pentagon is:
All ACT Math Resources































