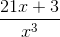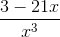How to add rational expressions with a common denominator
Help Questions
ACT Math › How to add rational expressions with a common denominator
Combine the following rational expressions:
Explanation
When working with complex fractions, it is important not to let them intimidate you. They follow the same rules as regular fractions!
In this case, our problem is made easier by the fact that we already have a common denominator. Nothing fancy is required to start. Simply add the numerators:
For our next step, we need to combine like terms. This is easier to see if we group them together.
Thus, our final answer is:
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Explanation
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Compute the following:
Explanation
Notice that the denominator are the same for both terms. Since they are both the same, the fractions can be added. The denominator will not change in this problem.
Simplify the following rational expression:
Explanation
Since both rational terms in the expression have the common denominator 
Simplify the following expression:
Explanation
Since both terms in the expression have the common denominator 
Simplify the following rational expression:
Explanation
Since both fractions in the expression have a common denominator of