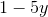All ACT Math Resources
Example Questions
Example Question #1 : Algebraic Fractions
Change to a mixed number
To convert from a fraction to a mixed number we must find out how many times the denominator goes into the numerator using division and the remainder becomes the new fraction.

Example Question #2 : Algebraic Fractions
What is the average of 

To average, we have to add the values and divide by two. To do this we need to find a common denomenator of 6. We then add and divide by 2, yielding 4.5/6. This reduces to 3/4.
Example Question #842 : Algebra
Which of the following is equivalent to 
None of the answers are correct
This problem is solved the same way ½ + 1/3 is solved. For example, ½ + 1/3 = 3/6 + 2/6 = 5/6. Find a common denominator then convert each fraction into an equivalent fraction using that common denominator. The final step is to add the two new fractions and simplify.
Example Question #645 : Algebra
A train travels at a constant rate of 

Set up the conversions as fractions and solve:
Example Question #3 : Algebraic Fractions
Simplify.
Can't be simplified
To simplify exponents which are being divided, subtract the exponents on the bottom from exponents on the top. Remember that only exponents with the same bases can be simplified
Example Question #4 : Algebraic Fractions
Simplify:
x2 – y2 can be also expressed as (x + y)(x – y).
Therefore, the fraction now can be re-written as (x + y)(x – y)/(x + y).
This simplifies to (x – y).
Example Question #5 : Algebraic Fractions
Simplify:
Notice that the 
Now multiply both the numerator and denominator by the conjugate of the denominator:
Example Question #11 : Algebraic Fractions
Simplify:
(2x + 4)/(x + 2)
x + 1
2
x + 4
2x + 2
x + 2
2
(2x + 4)/(x + 2)
To simplify you must first factor the top polynomial to 2(x + 2). You may then eliminate the identical (x + 2) from the top and bottom leaving 2.
Example Question #12 : Algebraic Fractions
Simplify the following expression:
Factor both the numerator and the denominator:
After reducing the fraction, all that remains is:
Example Question #13 : Algebraic Fractions
Simplify:
None of the other answers
With this problem the first thing to do is cancel out variables. The x2 can all be divided by each other because they are present in each system. The equation will now look like this:
Now we can see that the equation can all be divided by y, leaving the answer to be:
All ACT Math Resources