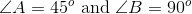All ACT Math Resources
Example Questions
Example Question #61 : Act Math
In a right triangle ABC, the measure of angle C is greater than 60 degrees. Which of the following statements could describe the measures of angles A and B?
Given that it is a right triangle, either angle A or B has to be 90 degrees. The other angle then must be less than 30 degrees, given that C is greater than 60 because there are 180 degrees in a triangle.
Example:
If angle C is 61 degrees and angle A is 90 degrees, then angle B must be 29 degrees in order for the angle measures to sum to 180 degrees.
Example Question #3 : Triangles
Right triangle 

Solving this problem quickly requires that we recognize how to break apart our ratio.
The Triangle Angle Sum Theorem states that the sum of all interior angles in a triangle is 
Since this is true, we can assume that 


Thus, 
To find the value of one angle of the ratio, simply assign fractional value to the sum of the ratios and multiply by 

Thus, the shortest angle (the one represented by 

Example Question #4 : Triangles
Right triangle 

The Triangle Angle Sum Theorem states that the sum of all interior angles in a triangle must be 


The rest is simple subtraction:
Thus, our missing angle is 
Example Question #5 : Triangles




The word similar means, comparable in measurement, but not equal. The best sides way to compare these two triangles is by looking at the diagonal side of the triangle since it cannot be mistaken for any of the other sides of either triangle. If the larger triangle has a measurement of 7 and the smaller triangle has a measurement of 3.5 for their diagonal sides, then that means the ratio of the larger triangle to the smaller one is 

This means that segment EF must be similar to segment AC (look at the orientation). So, since segment DE is similar to segment CB, divide 5 by two to get your answer.
Example Question #3 : Triangles
There are two similar right triangles. One has side lengths of 6, 8, and 10. The other has side lengths of 24, and 18. What is the length of the missing side?
1. Since the two triangles are similar, find the ratio of the two triangles to each other:
In this case, both triangles are multiples of a 
and
The ratio of the triangles is
2. Use the ratio you found to solve for 
Example Question #6 : Triangles
There are two right triangles, Triangle A and Triangle B. Triangle A has sides with lengths of 3, 4, and 5 and Triangle B has only two given side lengths: 3 and 4. The length of the hypotenuse is not given. Are these two triangles congruent?
Yes, because the missing hypotenuse length is 4.
It is impossible to say solely based on the provided information.
Yes, because the missing hypotenuse length is 5.
No, because you do not know the angle measures.
Yes, because the missing hypotenuse length is 5.
1. Find the length of the missing hypotenuse:
You can do this one of two ways:
1) Using the special 3-4-5 right triangle, you can infer that the missing hypotenuse is 5.
2) By using the Pythagorean Theorem, you can solve for the length of the hypotenuse:
In this case:
2. Using the meaning of congruent (the exact same three angles and sides), determine if these two triangles fit this meaning:
They do, because both are 3-4-5 right triangles, and thus must have corresponding and equal angles due to trigonometric properties.
Example Question #2 : How To Find The Area Of A Right Triangle
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
50
108
240
96
48
96
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Example Question #1 : How To Find The Area Of A Right Triangle
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
The base is equal to 6.
The height of an quilateral triangle is equal to 

Example Question #62 : Geometry
Find the area of the following right triangle to the nearest integer 
Note: The triangle is not necessarily to scale
None of the other answers
The equation used to find the area of a right triangle is: 

Using the given information, we can write 


Example Question #63 : Geometry

In the above triangle, if 

To find the area of a triangle use the formula:



All ACT Math Resources