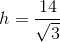All ACT Math Resources
Example Questions
Example Question #31 : Act Math
A regular pentagon has a side length of 
Because we're told the pentagon is a regular polygon, this means that all of its sides are the same length. That is, the side lengths are congruent.
In order to solve for the perimeter, which is the sum of all sides, we can use a multiplication shortcut of:




Using the information given in the problem, the values can be substituted in.
Note that this math is the same as adding 
Example Question #31 : Plane Geometry
The figure above is a pentagon. All of the angles listed (except the interior one) are exterior angles to the pentagon's interior angles.
What is the value of 
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
Solve for 
Example Question #32 : Act Math

The figure above is a pentagon. All of the angles listed (except the interior one) are exterior angles to the pentagon's interior angles.
What is the value of the largest unknown angle in the figure above?
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
Solve for 
Now, you have to find the largest unknown angle, which is 
Example Question #33 : Act Math
What is the sum of three angles in a pentagon?
The sum of all angles is determined by the following formula for a polygon:
In a pentagon, there are 5 sides, or 
There are 5 interior angles in a pentagon. Divide the total possible angle by 5 to determine the value of one interior angle.
Each interior angle of a pentagon is 108 degrees.
The sum of three angles in a pentagon is:
Example Question #1 : Hexagons

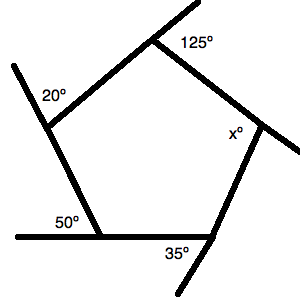
The figure above is a regular hexagon. 
What is the perimeter of the figure above?
You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the 



Now, the 




We know, then, that:
Or,
Now, this is only half of the size of the hexagon's side. Therefore, the full side length is 
Since this is a regular hexagon, all of the sides are of equal length. This means that your total perimeter is 

Example Question #2 : Hexagons
What is the perimeter of a regular hexagon with an area of 
The area of a regular hexagon is defined by the equation:


This is derived from the fact that the regular hexagon can be split up into 
To visualize this, consider the drawing:

Each triangle formed like this will be equilateral. It is easiest to remember this relationship and memorize the general area equation for equilateral triangles. (It is useful in many venues!)
So, for your data, you know:
Solving for 
This means that
Therefore, the perimeter of the figure is equal to 

Example Question #3 : Hexagons
Find the perimeter of a hexagon with a side length of 
There are 6 sides in a hexagon.
Therefore, given a side length of 16, the perimeter is:
Example Question #4 : Hexagons
The side length of a hexagon is 
Write the formula for the perimeter of a hexagon.
Substitute the given length.
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
The perimeter of a regular hexagon is 
To begin, calculate the side length of the hexagon. Since it is regular, its sides are of equal length. This means that a given side is 

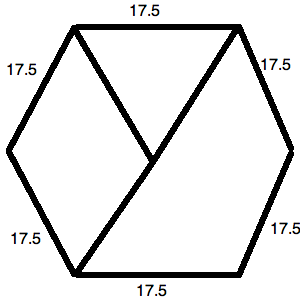
The little triangle at the top forms an equilateral triangle. This means that all of its sides are 


Example Question #2 : How To Find The Length Of The Diagonal Of A Hexagon
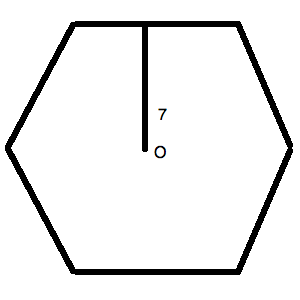
The figure above is a regular hexagon. O is the center of the figure. The line segment makes a perpendicular angle with the external side.
What is the length of the diagonal of the regular hexagon pictured above?
You could redraw your figure as follows. Notice that this kind of figure makes an equilateral triangle within the hexagon. This allows you to create a useful 

The 
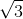


Therefore, we can say:
Solve for 
Rationalize the denominator:
Now, the diagonal of a regular hexagon is actually just double the length of this hypotenuse. (You could draw another equilateral triangle on the bottom and duplicate this same calculation set—if you wanted to spend extra time without need!) Thus, the length of the diagonal is:
Certified Tutor
All ACT Math Resources