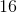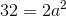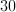All SAT Math Resources
Example Questions
Example Question #1 : 45/45/90 Right Isosceles Triangles
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
None of these
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
Example Question #1 : 45/45/90 Right Isosceles Triangles
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
50
200√2
100
100√2
50√2
100
Example Question #159 : Geometry
The length of the diagonal of a given square is 
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

Example Question #1 : Acute / Obtuse Triangles
Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?
0
10
15
30
The answer cannot be determined
10
The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.
Example Question #2 : How To Find If Two Acute / Obtuse Triangles Are Similar
A triangle with two equal angles is called a(n) __________.
equilateral triangle
disjoint triangle
Pythagoras triangle
isosceles triangle
right triangle
isosceles triangle
An isoceles triangle is a triangle that has at least two congruent sides (and therefore, at least two congruent angles as well).
Example Question #431 : Geometry
Triangle ABC has angle measures as follows:

What is 
79
44
57
90
19
57
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation
After combining like terms and cancelling, we have
Thus
Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
Example Question #162 : Sat Mathematics
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
Example Question #163 : Sat Mathematics
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
So the vertex angle is 40 and the base angles is 70
Example Question #1 : Acute / Obtuse Isosceles Triangles
The base angle of an isosceles triangle is 10 more than twice the vertex angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
The vertex angle is 32 degrees and the base angle is 74 degrees
Certified Tutor
All SAT Math Resources