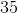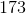All SAT Math Resources
Example Questions
Example Question #121 : Plane Geometry
In the figure above, line segments DC and AB are parallel. What is the perimeter of quadrilateral ABCD?
95
80
90
85
75
85
Because DC and AB are parallel, this means that angles CDB and ABD are equal. When two parallel lines are cut by a transversal line, alternate interior angles (such as CDB and ABD) are congruent.
Now, we can show that triangles ABD and BDC are similar. Both ABD and BDC are right triangles. This means that they have one angle that is the same—their right angle. Also, we just established that angles CDB and ABD are congruent. By the angle-angle similarity theorem, if two triangles have two angles that are congruent, they are similar. Thus triangles ABD and BDC are similar triangles.
We can use the similarity between triangles ABD and BDC to find the lengths of BC and CD. The length of BC is proportional to the length of AD, and the length of CD is proportional to the length of DB, because these sides correspond.
We don’t know the length of DB, but we can find it using the Pythagorean Theorem. Let a, b, and c represent the lengths of AD, AB, and BD respectively. According to the Pythagorean Theorem:
a2 + b2 = c2
152 + 202 = c2
625 = c2
c = 25
The length of BD is 25.
We now have what we need to find the perimeter of the quadrilateral.
Perimeter = sum of the lengths of AB, BC, CD, and DA.
Perimeter = 20 + 18.75 + 31.25 + 15 = 85
The answer is 85.
Example Question #112 : Plane Geometry
A traffic light hangs t feet from the ground, over a street. A man standing the shadow of the traffic light is h feet tall, and his shadow is s feet long. How far is the man standing from the spot on the street directly under the traffic light?
We can set this problem up like a set of similar triangles.
The first triangle is created by the three points: The Traffic light, the spot beneath the traffic light, and the spot where the man is standing (which is also the spot where the traffic light's shadow is).
The height of this Triangle is "T" as given in the question, and its base is the part that we are asked to solve for.
The second triangle is created by the top of the man's head, his feet, and the end of his shadow.
The height of this Triangle is "h" as given in the questions, and the base is "s".
We set up a proportion:
where X is the distance we are asked to find. Simply cross-multiply to solve.
Example Question #112 : Geometry

An meteor crashed in the desert and created an oblong shaped crater. Scientists want to find the width 

To calculate the width of the crater, use the given information to establish that the image draws similar triangles. When triangles that have corresponding angles and a ratio to their side lengths they are considered to be similar triangles.
Identify the known information.
therefore,

and the bases of the triangles are parallel.
Also,
Set up the side ratios for this particular problem.
Looking at the only full ratio that is given, the scalar multiplier can be found.
Therefore, to find the width of the crater 

Example Question #93 : Right Triangles
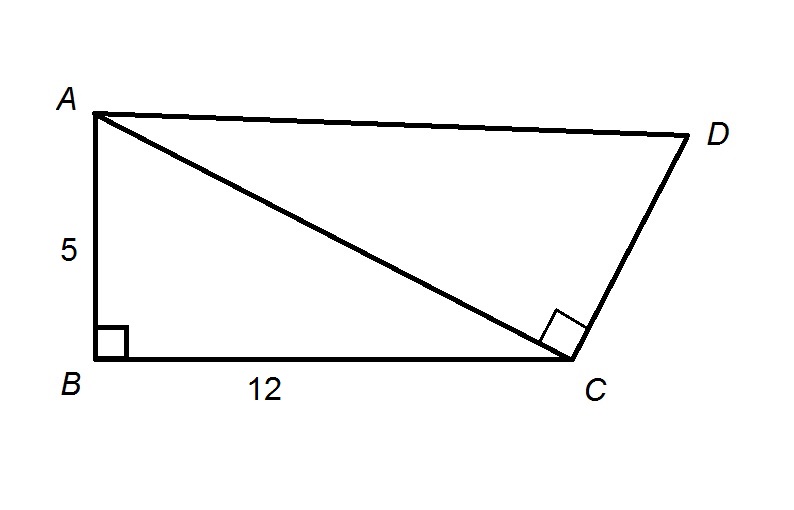
In the given diagram, 
By the Pythagorean Theorem,
Set 

Take the positive square root of both sides:

Set 

A right triangle has as its area half the product of the length of its legs, so the area of 
To the nearest whole number, this rounds to 35.
Certified Tutor
Certified Tutor
All SAT Math Resources