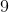All SAT II Math I Resources
Example Questions
Example Question #1 : Surface Area
A circular swimming pool has diameter 32 meters and depth 
None of the other responses is correct.
The bottom of the pool is a circle with diameter 32, and, subsequently, radius half this, or 16; its area is
The side of the pool is the lateral surface of a cylinder with radius 16 and height 
The area of the inside of the pool is the sum of these two, or
Example Question #101 : Geometry
A circular swimming pool at an apartment complex has diameter 50 feet and depth six feet throughout.
The apartment manager needs to get the interior of the swimming pool painted. The paint she wants to use covers 350 square feet per gallon. How many one-gallon cans of paint will she need to purchase?
The correct answer is not given among the other responses.
The pool can be seen as a cylinder with depth (or height) six feet and a base with diameter 50 feet - and radius half this, or 25 feet.
The bottom of the pool - the base of the cylinder - is a circle with radius 25 feet, so its area is

Its side - the lateral face of the cylinder - has area

Their sum - the total area to be painted - is 
Eight cans of paint and part of a ninth will be required, so the correct response is nine.
Example Question #2 : Surface Area

Figure not drawn to scale.
Find the surface area of the cylinder above.
94.25 in2
122.14 in2
56.55 in2
73.44 in2
87.25 in2
94.25 in2
In order to find the surface area of a cylinder, you need to find the surface areas of the circles that are the top and bottom of the cylinder (2 x pi x radius2) and add it to the surface are of the rectangle that is the side of the cylinder (diameter x height).
The surface area of the cylinder is 94.25 in2
Example Question #3 : Surface Area

Figure not drawn to scale
What is the surface area of the sphere above?
712.12 yd2
815.44 yd2
615.75 yd3
512.63 yd2
615.75 yd2
615.75 yd2

In order to find the surface area of a sphere, you must use the equation below:
The surface area of the sphere is 615.75 yd2
Example Question #1 : Advanced Geometry






The formula for the surface area of a cone is:

where 

Plugging in our values, we get:
Example Question #2 : Advanced Geometry
The surface area of cone 


To figure out 




This equation can be reduced to:
For a normal right angle cone, 

so
Our 
The height of cone 
Example Question #1 : Advanced Geometry
A circle of radius five is cut into two pieces, 

What is the area of the bottom?
When the smaller portion of the circle is curled in, it will make the top of a cone. The circumfrence of the circle on the bottom is 


Therefore we use the circumference formula to solve for our new r:
Substituting this value into the area formula, the area of the small circle becomes:
Example Question #2 : Advanced Geometry
A cone has a bottom area of 

The area of the bottom of the cone yields the radius,
The height of the cone is 
The area of the side of the cone is 

Example Question #1 : Advanced Geometry
If the surface area of a right angle cone 


Solving this problem is going to take knowledge of Algebra, Geometry, and the equation for the surface area of a cone: 


We can divide out 
We see this equation has taken the form of a quadratic expression, so to solve for 




This gives us solutions of 




Example Question #2 : Advanced Geometry
For a right circular cone 



To solve this problem, we will need to use the formula for finding the surface area of a cone, 





Certified Tutor
All SAT II Math I Resources