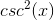All Precalculus Resources
Example Questions
Example Question #1 : Sum And Difference Identities For Tangent
According to the trigonometric identities,
Possible Answers:
Correct answer:
Explanation:
The trigonometric identity 
Some other identities that are important to know are:
Varun
Certified Tutor
Certified Tutor
University of Massachusetts Amherst, Bachelor of Science, Biochemistry and Molecular Biology.
Joyce
Certified Tutor
Certified Tutor
Iona College, Bachelor in Arts, Mathematics. Iona College, Master of Arts Teaching, Mathematics.
All Precalculus Resources
Popular Subjects
SAT Tutors in Atlanta, English Tutors in Chicago, GRE Tutors in Phoenix, ACT Tutors in Chicago, Reading Tutors in Seattle, Algebra Tutors in Miami, Math Tutors in Boston, Algebra Tutors in Dallas Fort Worth, Biology Tutors in Boston, GRE Tutors in Dallas Fort Worth
Popular Courses & Classes
SAT Courses & Classes in Seattle, MCAT Courses & Classes in New York City, ISEE Courses & Classes in Denver, ACT Courses & Classes in Denver, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Boston, LSAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Boston, LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston
Popular Test Prep
MCAT Test Prep in Denver, MCAT Test Prep in Chicago, ISEE Test Prep in Houston, ISEE Test Prep in Denver, LSAT Test Prep in Houston, LSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Seattle, SSAT Test Prep in Washington DC, ACT Test Prep in San Diego, ACT Test Prep in Los Angeles