All Common Core: 8th Grade Math Resources
Example Questions
Example Question #55 : Number Theory
Which of the following expressions is irrational?
An irrational number is defined as any number that cannot be expressed as a simple fraction or does not have terminating or repeating decimals. Of the answer choices given, the only number that cannot be expressed as a simple fraction or with repeating or terminating decimals is 
Example Question #2 : The Number System
Which of the following is an irrational number?
An irrational number is any number that can not be expressed as a ratio of integers, i.e. a fraction. Therefore, the only irrational number listed is 
Example Question #56 : Number Theory
Which of these expressions is not irrational?
The square root of an integer is either an irrational number or an integer. The latter is the case if and only if there is an integer which, when multiplied by itself, or squared, yields the number inside the symbol (the radicand) as the product. Of 
Example Question #61 : Number Theory
Which of the following represents an irrational number?
All of the answers are irrational
Pi is the only irrational number listed. Irrational numbers are in the form of infinite non-repeating decimals.
Example Question #61 : Number Theory
Which of the following is not an irrational number?
A root of an integer is one of two things, an integer or an irrational number. By testing all five on a calculator, only ![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214986/gif.latex)
Example Question #1 : Irrational Numbers
Which of the following is an irrational number?
An irrational number is any number that cannot be written as a fraction of whole numbers. The number pi and square roots of non-perfect squares are examples of irrational numbers.






Example Question #3 : The Number System
Of the following, which is a rational number?
A rational number is any number that can be expressed as a fraction/ratio, with both the numerator and denominator being integers. The one limitation to this definition is that the denominator cannot be equal to 
Using the above definition, we see 






Example Question #2 : Grade 8
Of the following, which is an irrational number?
The definition of an irrational number is a number which cannot be expressed in a simple fraction, or a number that is not rational.
Using the above definition, we see that 





This is an irrational number and our correct answer.
Example Question #4 : The Number System
Which of the following is NOT an irrational number?
Rational numbers are those which can be written as a ratio of two integers, or simply, as a fraction.
The solution of 


Example Question #5 : The Number System
Which of the following numbers is considered to be an irrational number?
An irrational number cannot be represented as the quotient of two integers.
Irrational numbers do not terminate and are not repeat numbers.
Looking at the possible answers,








Certified Tutor
Certified Tutor
All Common Core: 8th Grade Math Resources







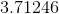










![\sqrt[2]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214959/gif.latex)
![\sqrt[4]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214960/gif.latex)
![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214958/gif.latex)
![\sqrt[5]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214961/gif.latex)
![\sqrt[6]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214962/gif.latex)























