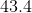All College Chemistry Resources
Example Questions
Example Question #1 : Calorimetry
Which of the following is true of a closed system?
A closed system does not allow for the exchange of matter or energy between the system and its surroundings.
A closed system allows for the exchange of matter and energy between the system and its surroundings.
A closed system allows for the exchange of energy between the system and its surroundings, but does not allow the exchange of matter.
A closed system allows for the exchange of matter between the system and its surroundings, but does not allow the exchange of energy.
A closed system contains no energy or matter and does not allow for the exchange of matter or energy between the system and its surroundings.
A closed system allows for the exchange of energy between the system and its surroundings, but does not allow the exchange of matter.
A closed system allows for the exchange of energy between the system and its surroundings, but does not allow the exchange of matter. This is the definition of a closed system. An open system allows for the exchange of both matter and energy between the system and its surroundings. An isolated system on the other hand does not allow the exchange of either matter or energy between the system and its surroundings.
Example Question #2 : Thermochemistry And Changes Of State
When 






Recall the following equation:
Now, since the bomb calorimeter keeps the volume constant, we know the following relationship:
Thus, we can then write the following equation for 
Start by finding 
From this, we know that
Now, find 
Your answer must have 
Example Question #2 : Solutions, States Of Matter, And Thermochemistry
How much heat energy is needed to raise the temperature of 



In this question, we're given the mass of copper, along with its specific heat capacity, and we're asked to determine the amount of heat energy necessary to increase its temperature by a given amount.
To solve this problem, we'll need to make use of the following equation.
Since we know what the values are for the mass and specific heat, we'll need to figure out what the temperature will be. Since the Kelvin and Celsius temperature scales both change by the same amount and only differ at their zero point, we can take the difference of the temperatures in degrees Celsius and use that value (since it will be equivalent to the change in the Kelvin temperature as well).
Plugging this information into the first expression, we can solve for the amount of heat energy that will bring this mass of copper to the desired temperature.
Example Question #31 : College Chemistry
Use average bond enthalpies to estimate the enthalpy change, in kilojoules, of the combustion of one mole of hexane 
| Type of Bond | Average bond enthalpy 
|
| Carbon-hydrogen single bond | 414 |
| Carbon-oxygen double bond | 736 |
| Oxygen-oxygen double bond | 498 |
| Oxygen-hydrogen single bond | 464 |
| Carbon-carbon single bond | 347 |
Start by writing the balanced equation for the combustion of hexane:
Recall the following equation:
Remember that energy is required to break bonds, so 

Next, draw out the Lewis structures of each molecule to figure out the number of bonds made or broken.
For the hexane, there are 
bonds that must be broken, and



For each oxygen, there is only 1 oxygen double bond to break. However, we will need to multiply this number by its stoichiometric coefficient.

For each carbon dioxide, there are 



For each water, there are 


Now, use the given information regarding to average bond enthalpies to find the change in enthalpy for the reaction.
Example Question #2 : Thermochemistry And Changes Of State
A 



Recall the equation that gives the relationship between change in temperature and amount of heat:

where 


Since the question asks for the final temperature, re-arrange the equation to solve for 
Substitute in the given values to solve for the final temperature.
Example Question #3 : Solutions, States Of Matter, And Thermochemistry
The specific heat capacity is defined as the amount of heat energy necessary to change a given amount of a substance by a certain temperature. Which of the following correctly expresses the units of specific heat capacity?
For this question, we're given a definition for the specific heat capacity of a substance and we're asked to identify the correct units for this term.
We can also recall the equation that relates all of these terms.
Rearranging this expression to isolate the term for the specific heat capacity gives us the following.
Next, we can recall what units would be appropriate to use for each of the following terms in the above expression. The 


Putting all this together gives us the following.
Example Question #31 : College Chemistry
How much heat is needed to raise the temperature of 10.0 g of water from 10.0 oC to 35.0 oC?
Specific heat capacity for water is
Recall the relationship between heat and specific heat capacity
Plug in known values and solve for Q
Example Question #32 : College Chemistry
An insulated container is filled with 50.0 g of water at 15.0 oC. 120.0 g of lead is heated to 100 oC and added to the insulated container. What is the final temperature of the system once it comes to equilibrium?
Specific heat of water is
Specific heat of lead is
Since Pb starts at a higher temperature than the water, we know that energy (in the form of heat) will be transferred from Pb to water. Due to the law of conservation of energy, the exact same amount of energy lost by Pb must be gained by water.
Recall that
Combining the two equations, we have
Combine like terms then solve for final temperature
Example Question #1 : Specific Heat Capacity
How much heat does it require to make a 



Recall the equation that gives the relationship between the change in temperature and the amount of heat:



Substitute in the given values to find how much heat is required to increase the temperature of the block of lead the specified amount.
Make sure to round the answer to three significant figures.
Example Question #1 : Phase Diagrams
Consider the typical phase diagram of a compound given below.
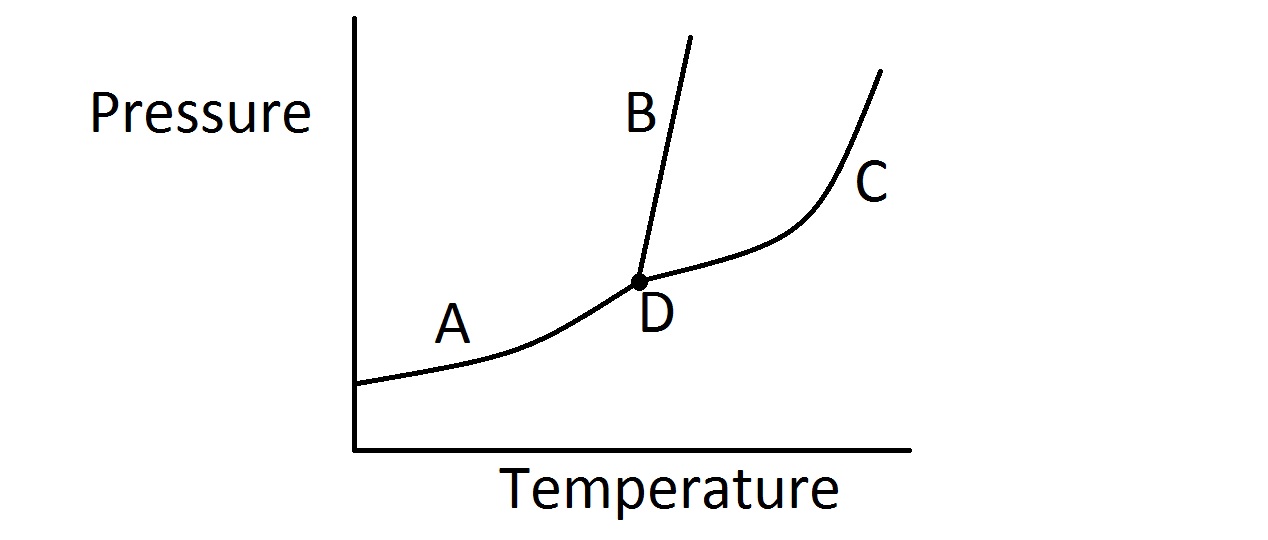
Which of the following lines or points on the diagram represents a situation in which the rate of vaporization of the compound is equal to its rate of condensation?
Line C
None of these
Line B
Point D
Line A
Line C
In this question, we're presented with a phase diagram and are asked to determine where on the graph the rate of vaporization equals the rate of condensation.
First, it's important to realize that when the rate of vaporization and condensation are equal, we have an equilibrium of liquid and gas phases. In other words, for a given temperature and pressure, the rate at which the liquid evaporates into a gas is exactly equal to the rate at which the gas condenses into a liquid.
On a phase diagram, the area of the upper left portion of the diagram represents the solid state. The middle portion of the diagram represents the liquid state. The bottom and right most part of the diagram represents the gas phase.
Furthermore, each line on the diagram represents the specific combination of temperature and pressure in which a given compound will exist in equilibrium between two phases. The point where all three lines intersect, however, represents the triple point. This tells us the temperature and pressure in which the compound will exist in an equilibrium between all three states.
Because we are looking for the equilibrium line that represents equilibrium of vaporization and condensation, we want the line that separates the liquid portion of the diagram from the gas portion. Based on the identification of regions on the diagram discussed above, that would be line C as shown in the diagram. Line A represents equilibrium between solid and gas (sublimation rate = deposition rate). Line B represents equilibrium between solid and liquid (melting rate = freezing rate).
Certified Tutor
All College Chemistry Resources