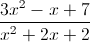All Algebra II Resources
Example Questions
Example Question #1 : Adding And Subtracting Rational Expressions
Simplify
This is a more complicated form of
Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators. Simplify as needed.
which is equivalent to
Simplify to get
Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
Simplify:
Because the two rational expressions have the same denominator, we can simply add straight across the top. The denominator stays the same.
Therefore the answer is 
Example Question #1 : Adding And Subtracting Rational Expressions
Simplify
The expression cannot be simplified.
a. Find a common denominator by identifying the Least Common Multiple of both denominators. The LCM of 3 and 1 is 3. The LCM of 



b. Write an equivialent fraction to 




The expression should now look like: 
c. Subtract the numerators, putting the difference over the common denominator.
Example Question #3 : Adding And Subtracting Rational Expressions
Combine the following expression into one fraction:
The two fractions cannot be combined as they have different denominators.
To combine fractions of different denominators, we must first find a common denominator between the two. We can do this by multiplying the first fraction by 

Since these fractions have the same denominators, we can now combine them, and our final answer is therefore:
Example Question #4 : Adding And Subtracting Rational Expressions
What is 
We start by adjusting both terms to the same denominator which is 2 x 3 = 6
Then we adjust the numerators by multiplying x+1 by 2 and 2x-5 by 3
The results are:
So the final answer is,
Example Question #561 : Intermediate Single Variable Algebra
What is 
Start by putting both equations at the same denominator.
2x+4 = (x+2) x 2 so we only need to adjust the first term:
Then we subtract the numerators, remembering to distribute the negative sign to all terms of the second fraction's numerator:
Example Question #1 : Solving Rational Expressions
Determine the value of 
(x+5)(x+3) is the common denominator for this problem making the numerators 7(x+3) and 8(x+5).
7(x+3)+8(x+5)= 7x+21+8x+40= 15x+61
A=61
Example Question #2 : Adding And Subtracting Rational Expressions
Add:
First factor the denominators which gives us the following:
The two rational fractions have a common denominator hence they are like "like fractions". Hence we get:
Simplifying gives us
Example Question #571 : Intermediate Single Variable Algebra
Subtract:
First let us find a common denominator as follows:
Now we can subtract the numerators which gives us :
So the final answer is
Example Question #162 : Equations / Inequalities
Solve the rational equation:
no solution



With rational equations we must first note the domain, which is all real numbers except 
The least common denominator or 







All Algebra II Resources