How to find the domain of a function
Help Questions
ACT Math › How to find the domain of a function
What is the domain of the function defined as follows:
Explanation
The domain is the set of all 


Thus 
Which of the following represents the domain of the function 
Explanation
You know that the square root function has real roots only for positive values. Therefore, you know that 
What is the domain of the following function?
Explanation
The two potential concerns for domain in a standard function are negative numbers inside even-powered radicals, and dividing by zero. In this case, the radical we have is odd-powered, so having a negative result underneath the radical is fine. All we need to do, then, is avoid dividing by zero, which means avoiding a result which sums to zero under the radical. In this case, only 
Thus, our domain is
Find the domain of the function:
All real numbers except for 1
All real numbers
All real numbers except for –2
0
Explanation
If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into
and then cancelling the 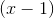
This new expression, 



Thus the domain of the function is all 
What is the domain of the given function?
x ≠ –3
All real numbers
x ≠ 3, –3
x ≠ 3
x ≠ 0
Explanation
The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.
What is the domain of 
Explanation
The domain of the function 

Therefore, for the function given, 


So the domain must be 
What is the domain of 
Explanation
To find the domain we want to find any areas for which an x value will not work in our function. The potential problem area would be that under the radical.
Therefore, for the function given, 


So the domain must be 
In other words, there is no real value of 

Find the domain of the following function:
Explanation
To find the domain, you must find the values for which you can plug in for 


Thus,
Therefore, for our function, 


Which of the following represents the domain of 

Explanation
Using our properties of exponents, we could rewrite 
This means that when we input 

The first step is to subtract 2 from 

Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function 





Find the domain of the given function:
All real numbers
All real numbers x such that x ≠ 1, 0
All real numbers x such that x ≠ 3, 0
All real numbers x such that x ≠ 3
All real numbers x such that x ≠ 0
Explanation
When x = 0 or x = 3, the function is undefined due to its denominator.
Thus the domain is all real numbers x, such that x is not equal to 0 or 3.

![t = [-\infty,-2)\cup (-2,2)\cup (2,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/414770/gif.latex)


![[-\infty,0)\cup(0,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/414773/gif.latex)
![[-\infty,2)\cup(2,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/414774/gif.latex)

![t = [-\infty,-2)\cup (-2,2)\cup (2,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/414827/gif.latex)







![f(x) = \frac{4-x}{\sqrt[3]{3+x}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/504166/gif.latex)




![(-\infty, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/504155/gif.latex)




























![\sqrt[5]{(x-2)^{4}}+3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/186063/gif.latex)
