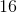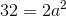All SAT Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
None of these
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
Example Question #1 : 45/45/90 Right Isosceles Triangles
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
50√2
100√2
100
200√2
50
100
Example Question #159 : Geometry
The length of the diagonal of a given square is 
If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.
We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.
Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:
Now, solve for the unknown:

This means that the length of the sides of our triangle, as well as the sides of our square, is 
To find the area of the square, do the following:

Certified Tutor
Certified Tutor
All SAT Math Resources