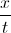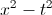How to divide rational expressions
Help Questions
SAT Math › How to divide rational expressions
Which of the following is equivalent to 
Explanation
We will need to simplify the expression 


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

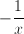


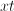
In order to convert the fraction 
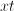

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction 

To simplify this further, we can think of 


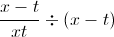
Lastly, we will use the property of exponents which states that, in general, 
The answer is