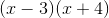Algebra
Help Questions
PSAT Math › Algebra
Multiply the binomial.
Explanation
By multiplying with the foil method, we multiply our first values giving 


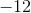
Multiply the binomial.
Explanation
By multiplying with the foil method, we multiply our first values giving 


The maximum number of sweaters that Lauren can sew every day is equal to s, and the amount, in cents, that she charges for each sweater is equal to c. Which of the following expressions is equivalent to the maximum amount of money that Lauren can make, in dollars, after three weeks?
3_c_/(100_s_)
2100_sc_
21_sc_/100
2100_s_/c
300_c_/s
Explanation
The amount of money that Lauren can make depends on the number of sweaters that she can make. If she makes at most s sweaters a day, then we can multiply the number of days that she works by s to determine the total number of sweaters she makes.
total number of sweaters = (s)(number of days)
We are told to consider a time interval of three weeks. Because there are seven days in one week, the number of days over this period of time would equal 3(7), or 21 days. In other words, there are 21 days in three weeks Thus, the number of sweaters is equal to the product of s and 21.
total number of sweaters = (s)(21)
Now that we have the number of sweaters Lauren can make, we can multiply this by the cost of each sweater, which is equal to c cents, in order to obtain the amount of money she eared.
amount of money earned = (number of sweaters)(cost of each sweater)
amount of money earned = s(21)(c)
However, because the price of each sweater is given in terms of cents, the amount of money s(21)(c) will be equal to the number of cents she makes. The question, though, asks us to find the amount of money in dollars. We must use a conversion factor to change the number of cents to dollars. Remember that there are 100 cents per dollar.
Give the lines y = 0.5x+3 and y=3x-2. What is the y value of the point of intersection?
2
3
4
6
7
Explanation
In order to solve for the x value you set both equations equal to each other (0.5x+3=3x-2). This gives you the x value for the point of intersection at x=2. Plugging x=2 into either equation gives you y=4.
Give the coefficient of 

Explanation
If the expression 

or, equivalently, the coefficient of 
Therefore, the 
Find all possible zeros for the following function.


Explanation
To find the zeros of the function, use factoring.
Set up the expression in factored form, leaving blanks for the numbers that are not yet known.
At this point, you need to find two numbers - one for each blank. By looking at the original expression, a few clues can be gathered that will help find the two numbers. The product of these two numbers will be equal to the last term of the original expression (-1, or c in the standard quadratic formula), and their sum will be equal to the coefficient of the second term of the original expression (0, or b in the standard quadratic formula). Because their product is negative (-1) and the sum is zero, that must mean that they have different signs but the same absolute value.
Now, at this point, test a few different possibilities using the clues gathered from the original expression. In the end, it's found that the only numbers that work are 1 and -1, as the product of 1 and -1 is -1, and sum of 1 and -1 is 0. So, this results in the expression's factored form looking like...
This is known as a difference of squares.
From here, set each binomial equal to zero and solve for 
and
To verify the zeros, graph the original function and identify where the graph touches or crosses the x-axis.

Therefore the zeros of the function are,
According to Heron's Formula, the area of a triangle with side lengths of a, b, and c is given by the following:
where s is one-half of the triangle's perimeter.
What is the area of a triangle with side lengths of 6, 10, and 12 units?
12√5
4√14
8√14
14√2
48√77
Explanation
We can use Heron's formula to find the area of the triangle. We can let a = 6, b = 10, and c = 12.
In order to find s, we need to find one half of the perimeter. The perimeter is the sum of the lengths of the sides of the triangle.
Perimeter = a + b + c = 6 + 10 + 12 = 28
In order to find s, we must multiply the perimeter by one-half, which would give us (1/2)(28), or 14.
Now that we have a, b, c, and s, we can calculate the area using Heron's formula.
What property of arithmetic is demonstrated here?
Reflexive
Transitive
Commutative
Identity
Symmetric
Explanation
The statement expresses the idea that any number is equal to itself. This is the reflexive property of equality.
Factor the following equation.
x2 – 16
(x + 4)(x + 4)
(x – 4)(x – 4)
(x + 4)(x – 4)
(x)(x – 4)
(x2)(4 – 2)
Explanation
The correct answer is (x + 4)(x – 4)
We neen to factor x2 – 16 to solve. We know that each parenthesis will contain an x to make the x2. We know that the root of 16 is 4 and since it is negative and no value of x is present we can tell that one 4 must be positive and the other negative. If we work it from the multiple choice answers we will see that when multiplying it out we get x2 + 4x – 4x – 16. 4x – 4x cancels out and we are left with our answer.
Use FOIL to simplify the following product:
Explanation
Use the FOIL method (first, outside, inside, last) to find the product of:
First:
Outside:
Inside:
Last:
Sum the products to find the polynomial: