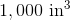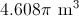All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Volume Of A Cone
A cone has height 18 inches; its base has radius 4 inches. Give its volume in cubic feet (leave in terms of 
Convert radius and height from inches to feet by dividing by 12:
Height: 18 inches = 
Radius: 4 inches =
The volume of a cone is given by the formula
Substitute 
Example Question #21 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
Give the volume of a cone whose height is 10 inches and whose base is a circle with circumference 
A circle with circumference 

The area of the base is therefore

To find the volume of the cone, substitute 

Example Question #21 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
The height of a cone and the radius of its base are equal. The circumference of the base is 
A circle with circumference 

The height is also 


Example Question #1 : How To Find The Volume Of A Cone
You are an architect designing a cone shaped structure. If the structure will be 30 ft tall and 10 feet wide at the base, what will the volume of the structure be?
You are an architect designing a cone shaped structure. If the structure will be 30 ft tall and 10 feet wide at the base, what will the volume of the structure be?
Begin by using the formula for volume of a cone:
Now, we simply need to plug in our knowns.
We know the height is 30 ft.
We know that the diameter is 10ft, however, we need the radius.
Divide 10 by 2 to get a radius of 5 ft.
Now, let's go....
Example Question #2 : How To Find The Volume Of A Cone
Find the volume of a cone with the following measurements:
- diameter = 12in
- height = 6in
To find the volume of a cone, we will use the following formula:
where r is the radius and h is the height of the cone.
Now, we know the diameter of the cone is 12in. We also know the diameter is two times the radius. Therefore, the radius is 6in.
We know the height of the cone is 6in.
Knowing all of this, we can substitute into the formula. We get
Example Question #1 : How To Find The Volume Of A Cone
Find the volume of a cone with the following measurements:
Diameter: 14in
Height: 9in
To find the volume of a cone, we will use the following formula:
where r is the radius and h is the height of the cone.
Now, we know the diameter of the cone is 14in. We also know the diameter is two times the radius. Therefore, the radius is 7in.
We know the height of the cone is 9in.
Knowing all of this, we can substitute into the formula. We get
Example Question #4 : How To Find The Volume Of A Cone
Find the volume of a cone with the following measurements:
- height: 12in
- diameter: 6in
To find the volume of a cone, we will use the following formula:
where r is the radius and h is the height of the cone.
Now, we know the height of the cone is 12in. We also know the diameter of the cone is 6in. We know the diameter is two times the radius. Therefore, the radius is 3in.
So, we get
Example Question #421 : Geometry
Find the volume of a cone with a base diameter of 2, and a height of 10.
Write the formula to find the volume of a cone.
The diameter is 2, which means the radius is 1. Substitute the known dimensions.
The answer is:
Example Question #1 : How To Find The Volume Of A Cone
A cone has height 240 centimeters; its base has radius 80 centimeters. Give its volume in cubic meters.
Convert both dimensions from centimeters to meters by dividing by 100:
Height: 240 centimeters = 
Radius: 80 centimeters = 
Substitute 
Certified Tutor
All ISEE Upper Level Math Resources