Spheres
Help Questions
Geometry › Spheres
If the diameter of a sphere is 
Explanation
The radius is half the length of a diameter.
Write the formula for the surface area of a sphere and plug in the radius.
Find the surface area of a hemisphere if it has a radius of 
Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.
Recall how to find the surface area of a sphere:


Now, since the sphere is cut in half, it also has a circle as its base.
Recall how to find the area of a circle:
Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.
Plug in the given radius to find the surface area.
Make sure to round to 
If the volume of a sphere is 
Explanation
The correct answer is 6.12 ft.
Plug the value of 
Multiply both sides by 3 to get
Then divide both sides by 
Then take the 3rd root of both sides to get 3.06 ft for the radius. Finally, you have to multiply by 2 on both sides to get the diameter. Thus
What is the volume of a sphere with a diameter of 6 in?
Explanation
The formula for the volume of a sphere is:
where 
If the volume of a sphere is 
Explanation
The correct answer is 6.12 ft.
Plug the value of 
Multiply both sides by 3 to get
Then divide both sides by 
Then take the 3rd root of both sides to get 3.06 ft for the radius. Finally, you have to multiply by 2 on both sides to get the diameter. Thus
Find the surface area for a hemisphere that has a radius of 
Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.
Recall how to find the surface area of a sphere:


Now, since the sphere is cut in half, it also has a circle as its base.
Recall how to find the area of a circle:
Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.
Plug in the given radius to find the surface area.
Make sure to round to 
If the radius of the sphere is one half, what is the surface area?
Explanation
Write the formula for the surface area of a sphere, plug in the radius, and find the area.
Find the surface area of a sphere if the volume is 
Explanation
Write the formula for the volume of a sphere and substitute volume to find radius.
Write the formula for the surface area of a sphere and plug in the radius.
Find the surface area of a hemisphere that has a radius of 
Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.
Recall how to find the surface area of a sphere:


Now, since the sphere is cut in half, it also has a circle as its base.
Recall how to find the area of a circle:
Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.
Plug in the given radius to find the surface area.
Make sure to round to 
Find the surface area of a hemisphere that has a radius of 
Explanation

In order to find the area of a hemisphere, which is just half a sphere, you will need to first find half the surface area of the sphere.
Recall how to find the surface area of a sphere:


Now, since the sphere is cut in half, it also has a circle as its base.
Recall how to find the area of a circle:
Now add together half the surface area of a sphere with the area of the circular base to find the surface area of a hemisphere.
Plug in the given radius to find the surface area.
Make sure to round to 

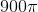

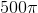








































![\sqrt[3]{9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/296151/gif.latex)


![\sqrt[3]{\frac{3\pi}{4}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/296154/gif.latex)



![r=\sqrt[3]{\frac{3}{4\pi}}= (\frac{3}{4\pi})^\frac{1}{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/296162/gif.latex)
![A=4\pi r^2 = 4\pi \left[\left(\frac{3}{4\pi}\right)^\frac{1}{3}\right]^2 = 4\pi\left(\frac{3}{4\pi}\right)^\frac{2}{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/299046/gif.latex)













