All AP Physics C Electricity Resources
Example Questions
Example Question #21 : Electricity

Three equal point charges 

Draw a line from the center perpendicular to any side of the triangle. This line divides the side into two equal pieces of length 


Example Question #21 : Electricity

A uniformly charged hollow disk has inner radius 



Use a polar coordinate system with surface charge density 



Example Question #21 : Electricity And Magnetism Exam

Two point charges 




By the Pythagorean theorem, the distance from point P to charge 



Example Question #181 : Ap Physics C

A nonuniformly charged ring of radius 

Use a polar coordinate system, the given linear charge density 


Example Question #21 : Electricity And Magnetism Exam

In this model of a dipole, two charges 






By the law of cosines, the distance from the point to charge 

The distance to charge 




Lastly, the exact potential is given by

Remark: Far from the dipole (approximating 

Example Question #181 : Ap Physics C

A uniformly charged hollow spherical shell of radius 



Use a spherical coordinate system and place the point of interest a distance 



.
Remarkably, this is the same potential that would exist a distance 
Example Question #181 : Ap Physics C

A thin bar of length L lies in the xy plane and carries linear charge density 



Use the linear charge density 



Example Question #182 : Ap Physics C

A uniformly charged ring of radius 


Use the linear charge density 





Example Question #181 : Ap Physics C

A uniformly charged square frame of side length 

You may wish to use the integral:
Calculate the potential due to one side of the bar, and then multiply this by 


All AP Physics C Electricity Resources















![=\frac{1}{2\pi\epsilon_0}\frac{Q}{R_2^2-R_1^2}\left[\sqrt{r^2+a^2} \right ]_{R_1}^{R_2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891652/gif.latex)
















![=\frac{b}{4\pi\epsilon_0}\left [\frac{\theta}{2}-\frac{\sin2\theta}{4} \right ]_{0}^{2\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891167/gif.latex)













![=\frac{1}{4\pi\epsilon_0} \left (\frac{Q}{2} \right ) \left [\frac{1}{Ra}\sqrt{R^2 + a^2-2Ra\cos\theta} \right ]_{0}^{\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/890844/gif.latex)









![= \frac{b}{4\pi\epsilon_0}\left [ \sqrt{x^2+a^2}\right ]_{0}^{L}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891578/gif.latex)













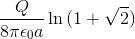


![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)





