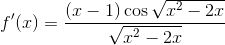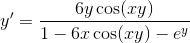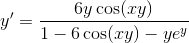Derivatives
Help Questions
AP Calculus AB › Derivatives
Find
Explanation
We are going to use three rules along with the chain rule:
So then, using our first rule and the chain rule
then using our second rule and chain rule
then using our third rule (no chain rule this time)
Then we rearrange the equation for simplification,

and
Find the derivative of
None of these answers
Explanation
The chain rule of the derivative always deals with the composition of two or more functions.
In this case we can identify two,
and

So 
With chain rule, you always start on the outermost function and work your way inward, which in this case is:
Always the derivative of the outermost evaluated at the inner, multiplied by the derivative of the inner.
Find 
Explanation
Let
Then
can be rewritten as
Let
The function can now be rewritten as
Applying the chain rule twice:
Explanation
Explanation
Explanation
Explanation
Determine the rate of change of the angle opposite the base of a right triangle -whose length is increasing at a rate of 1 inch per minute, and whose height is a constant 2 inches - when the area of the triangle is 2 square inches.




Explanation
To determine the rate of the change of the angle opposite to the base of the given right triangle, we must relate it to the rate of change of the base of the triangle when the triangle is a certain area.
First we must determine the length of the base of the right triangle at the given area:
Now, we must find something that relates the angle opposite of the base to the length of the base and height - the tangent of the angle:
To find the rate of change of the angle, we take the derivative of both sides with respect to time, keeping in mind that the base of the triangle is dependent on time, while the height is constant:
We know the rate of change of the base, and we can find the angle from the sides of the triangle:
Plugging this and the other known information in and solving for the rate of change of the angle adjacent to the base, we get

Find the derivative of the following function at the point 
Explanation
Use the power rule on each term of the polynomial to get the derivative,
Now we plug in
Given that 
Explanation
To find the derivative of the function, we use implicit differentiation, which is an application of the chain rule. We use this because 



First, we use the chain rule combined with the product rule in taking the derivative of y
Then we expand in order to isolate the terms with
Then we factor out a