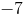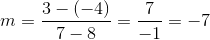How to find the slope of a line
Help Questions
ACT Math › How to find the slope of a line
What is the slope of a line which passes through coordinates 

Explanation
Slope is found by dividing the difference in the 

What is the slope of a line that passes though the coordinates 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of a line running through points 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of the line defined by the equation 
Explanation
The easiest way to find the slope of a line based on its equation is to put it into the form 

Start with your original equation 
Now, subtract 
Next, subtract 
Finally, divide by 
This is the same as:
Thus, the slope is 
What is the slope of the line defined as 
Explanation
To calculate the slope of a line from an equation of the line, the easiest way to proceed is to solve it for 



Next you merely need to divide by 
Thus, the slope is
What is the slope of the line perpendicular to 
Explanation
To begin, it is easiest to find the slope of a line by putting it into the form 


Now, recall that perpendicular lines have slopes of opposite sign and reciprocal numerical value. Thus, if our slope is 

What is the slope of the line represented by the equation 
Explanation
The slope of an equation can be calculated by simplifying the equation to the slope-intercept form 
Since 

This can be further simplified to


In this scenario, 

If 2x – 4y = 10, what is the slope of the line?
–5/2
2
–0.5
0.5
–2
Explanation
First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.
What is the slope of the line with equation 4_x_ – 16_y_ = 24?
1/4
1/8
–1/4
–1/8
1/2
Explanation
The equation of a line is:
y = mx + b, where m is the slope
4_x_ – 16_y_ = 24
–16_y_ = –4_x_ + 24
y = (–4_x_)/(–16) + 24/(–16)
y = (1/4)x – 1.5
Slope = 1/4
What is the slope of the line represented by the equation 
Explanation
To rearrange the equation into a 

First, add 

Then, divide both sides by 6 to get 
If you divide each part of the numerator by 6, you get