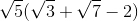All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Common Factor Of Square Roots
To solve the equation 
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
Example Question #1 : How To Find The Common Factor Of Square Roots
Solve for 
First, we can simplify the radicals by factoring.
Now, we can factor out the 
Now divide and simplify.
Example Question #2 : How To Find The Common Factor Of Square Roots
Which of the following is equivalent to:

To begin with, factor out the contents of the radicals. This will make answering much easier:
They both have a common factor 
This is the same as:
These have a common 
Example Question #22 : Arithmetic
Simplify:
These three roots all have a 
Now, this could be rewritten:
Now, note that
Therefore, you can simplify again:
Now, that looks messy! Still, if you look carefully, you see that all of your factors have 
This is the same as:
Example Question #21 : Arithmetic
Simplify:
Begin by factoring out the relevant squared data:

This can be simplified to:
Since your various factors contain square roots of 
Technically, you can factor out a 
Example Question #4 : How To Find The Common Factor Of Square Roots
Solve for 
Begin by breaking apart the square roots on the left side of the equation:
This can be rewritten:
You can combine like terms on the left side:
Solve by dividing both sides by 
This simplifies to:
Example Question #5 : How To Find The Common Factor Of Square Roots
Solve for 
To begin solving this problem, find the greatest common perfect square for all quantities under a radical.

Pull 

Next, factor out 

Lastly, isolate 

Example Question #6 : How To Find The Common Factor Of Square Roots
Solve for 
Solving this one is tricky. At first glance, we have no common perfect square to work with. But since each term can produce the quantity 

Simplify the first term:

Divide all terms by 

Next, factor out 

Isolate 


Last, simplify the denominator:

Example Question #7 : How To Find The Common Factor Of Square Roots
Solve for 
Right away, we notice that 

Our first step then becomes simplifying the equation by dividing everything by 

Next, factor out 

Lastly, isolate 

Example Question #8 : How To Find The Common Factor Of Square Roots
Solve for 
Once again, there are no common perfect squares under the radical, but with some simplification, the equation can still be solved for 

Simplify:

Factor out 

Lastly, isolate 

Certified Tutor
All ACT Math Resources