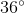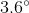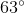Other Quadrilaterals
Help Questions
SAT Math › Other Quadrilaterals
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
I only
II only
I and II only
II and III only
I, II, and III
Explanation
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
I only
II only
I and II only
II and III only
I, II, and III
Explanation
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
If a polygon has 10 sides, what is the measure of each exterior angle?
Explanation
In order to figure this out, we need to remember the formula for finding exterior angles. 
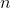
So the measure of each exterior angle is 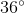
If a polygon has 10 sides, what is the measure of each exterior angle?
Explanation
In order to figure this out, we need to remember the formula for finding exterior angles. 
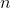
So the measure of each exterior angle is