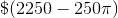How to find the area of a sector
Help Questions
SAT Math › How to find the area of a sector
Explanation
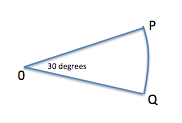
First, we figure out what fraction of the circle is contained in sector OPQ: 

Using the formula for the area of a circle, 

We can use this to solve for the circumference of the circle, 

Now, OP and OQ are both equal to r, and PQ is equal to 
To get the perimeter, we add OP + OQ + PQ, which give us 

If B is a circle with line AC = 12 and line BC = 16, then what is the area formed by DBE?
Explanation
Line AB is a radius of Circle B, which can be found using the Pythagorean Theorem:
Since AB is a radius of B, we can find the area of circle B via:
Angle DBE is a right angle, and therefore 

The radius of the circle above is 

Explanation
Area of Circle = πr2 = π42 = 16π
Total degrees in a circle = 360
Therefore 45 degree slice = 45/360 fraction of circle = 1/8
Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π
A central angle of a circle measures 60 degrees. If its corresponding arc measures 3 units, what is the area of the circle?
Explanation
If the central angle measures 60 degrees, divide the 360 total degrees in the circle by 60.
Multiply this by the measure of the corresponding arc to find the total circumference of the circle.
Use the circumference to find the radius, then use the radius to find the area.

The arc from 


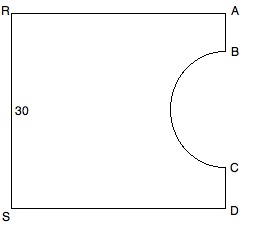
All units are in feet.
The diagram shows a plot of land.
The cost of summer upkeep is $2.50 per square foot.
In dollars, what is the total upkeep cost for the summer?
Explanation
To solve this, we must begin by finding the area of the diagram, which is the area of the square less the area of the semicircle.
The area of the square is straightforward:
30 * 30 = 900 square feet
Because each side is 30 feet long, AB + BC + CD = 30.
We can substitute BC for AB and CD since all three lengths are the same:
BC + BC + BC = 30
3BC = 30
BC = 10
Therefore the diameter of the semicircle is 10 feet, so the radius is 5 feet.
The area of the semi-circle is half the area of a circle with radius 5. The area of the full circle is 52π = 25π, so the area of the semi-circle is half of that, or 12.5π.
The total area of the plot is the square less the semicircle: 900 - 12.5π square feet
The cost of upkeep is therefore 2.5 * (900 – 12.5π) = $(2250 – 31.25π).
A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in2, what is the surface area of one piece of pizza?
36π in2
144π in2
9π in2
4.5π in2
18π in2
Explanation
The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s2. Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).
Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 62 = 36π in2. If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in2.
 what is the perimeter of sector?
what is the perimeter of sector?