All Introduction to Analysis Resources
Example Questions
Example Question #1 : Ordered Field And Completeness Axioms
Identify the following property.
On the space 





Multiplicative Property
Distributive Law
Trichotomy Property
Existence of Multiplicative Identity
Transitive Property
Trichotomy Property
The real number system, 
The properties are as follows.
Trichotomy Property:
Given 




Transitive Property:
For 





Additive Property:
For 





Multiplicative Properties:
For 








Therefore looking at the options the Trichotomy Property identifies the property in this particular question.
Example Question #2 : Intro Analysis
Identify the following property.
For 





Multiplicative Properties
Distribution Laws
Additive Property
Transitive Property
Trichotomy Property
Transitive Property
The real number system, 
The properties are as follows.
Trichotomy Property:
Given 




Transitive Property:
For 





Additive Property:
For 





Multiplicative Properties:
For 








Therefore looking at the options the Transitive Property identifies the property in this particular question.
Example Question #1 : Intro Analysis
Identify the following property.
For 





Trichotomy Property
Distribution Laws
Transitive Property
Multiplicative Properties
Additive Property
Additive Property
The real number system, 
The properties are as follows.
Trichotomy Property:
Given 




Transitive Property:
For 





Additive Property:
For 





Multiplicative Properties:
For 








Therefore looking at the options the Additive Property identifies the property in this particular question.
Example Question #1 : The Real Number System
Identify the following property.
For 








Transitive Property
Additive Property
Distribution Laws
Multiplicative Properties
Trichotomy Property
Multiplicative Properties
The real number system, 
The properties are as follows.
Trichotomy Property:
Given 




Transitive Property:
For 





Additive Property:
For 





Multiplicative Properties:
For 








Therefore looking at the options the Multiplicative Properties identifies the property in this particular question.
Example Question #3 : Intro Analysis
Determine whether the following statement is true or false:
If 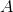



True
False
True
According to the Well-Ordered Principal this statement is true. The following proof illuminate its truth.
Suppose 


Therefore, by the Completeness Axiom the supremum of 
Furthermore, if 


Thus by the Reflection Principal,

exists and

Therefore proving the statement in question true.
Example Question #2 : Intro Analysis
What term does the following define.
A sequence of sets 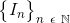

Nested
Increasing
Bounded
Decreasing
Unbounded
Nested
This statement:
A sequence of sets 
is the definition of nested.
This means that the sequence 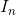


Other theorems in intro analysis build off this understanding.
Example Question #2 : Intro Analysis
Determine whether the following statement is true or false:
Let 



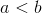


True
False
False
Determine this statement is false by showing a contradiction when actual values are used.
Let
First make sure the inequalities hold true.

and
Now find the products.
Therefore, the statement is false.
Example Question #4 : Intro Analysis
What conditions are necessary to prove that the upper and lower integrals of a bounded function exist?









![f:[a,b]\rightarrow \mathbb{Z}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019575/gif.latex)



![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019583/gif.latex)



![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019563/gif.latex)



![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019563/gif.latex)
Using the definition for Riemann sums to define the upper and lower integrals of a function answers the question.
According the the Riemann sum where 

1. The upper integral of 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019627/gif.latex)


![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019630/gif.latex)
2. The lower integral of 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019632/gif.latex)


![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019635/gif.latex)
3. If 1 and 2 are the same then the integral is said to be
if and only if 


![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019640/gif.latex)
Therefore the necessary condition for the proving the upper and lower integrals of a bounded function exists is if and only if 


![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019644/gif.latex)
Example Question #5 : Intro Analysis
What term has the following definition.



![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019833/gif.latex)

Refinement of a partition
Norm
Upper Riemann sum
Lower Riemann sum
Partition
Partition
By definition
If 


A partition over the interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019839/gif.latex)


Therefore, the term that describes this statement is partition.
Example Question #3 : Intro Analysis
What term has the following definition.
The __________ of a partition 
Lower Riemann sum
Upper Riemann Sum
Refinement of a partition
Norm
Partition
Norm
By definition
If 


A partition over the interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019847/gif.latex)


Furthermore,
The norm of the partition

Therefore, the term that describes this statement is norm.
All Introduction to Analysis Resources





![f:[a,b]\rightarrow \mathbb{R}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019569/gif.latex)
![f:[a,b]\rightarrow \mathbb{Z}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1019579/gif.latex)







